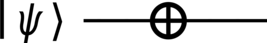Circuits#

In Qhronology, quantum circuits are created as instances of the QuantumCircuit class:

from qhronology.quantum.circuits import QuantumCircuit

In the circuit diagram picturalism of these structures, time increases from left to right, and so the preparation of input states (created as instances of the QuantumState class and its derivatives) begins in the past (on the left) while the measurement (or postselection) of output states occurs in the future (on the right). Operations on these states are represented by quantum gates (created as instances of the various subclasses of the QuantumGate base class), and all of these events are connected by quantum wires describing the flow of quantum information (i.e., quantum probabilities) through time.

Main class#

Bases: SymbolicsProperties

A class for creating quantum circuits and storing their metadata.

Instances provide complete descriptions of quantum circuits, along with various associated attributes (such as mathematical conditions, including normalization). The circuit’s input is recorded as a list of QuantumState objects, with the composition of the elements of this forming the total input. Similarly, the circuit’s transformation on its input is recorded as a list of QuantumGate objects, with the product of the (linear) elements of this list forming the total transformation (e.g., unitary matrix).

Parameters:

inputs (list[QuantumState]) – An ordered list of QuantumState instances. The total input state is the tensor product of these individual states in the order in which they appear in inputs. Must all have the same value of the dim property. Defaults to [].
gates (list[QuantumGate]) – An ordered list of QuantumGate instances. The total gate is the product of these individual gates in the order in which they appear in gates. Must all have the same values of the dim and num_systems properties. Defaults to [].
traces (list[int]) – The numerical indices of the subsystems to be traced over. Defaults to [].
postselections (list[tuple[mat | arr | QuantumObject, int | list[int]]]) – A list of 2-tuples of vectors or matrix operators paired with the first (smallest) index of their postselection target systems. Must all have the same value of the dim property. Defaults to [].
symbols (dict[sym | str, dict[str, Any]]) – A dictionary in which the keys are individual symbols and the values are dictionaries of their respective SymPy keyword-argument assumptions. The value of the symbols property of all states in inputs and gates in gates are automatically merged into the instance’s corresponding symbols property. Defaults to {}.
conditions (list[tuple[num | sym | str, num | sym | str]]) – A list of \(2\)-tuples of conditions to be applied to all objects (such as states and gates) computed from the circuit. All instances of the expression in each tuple’s first element are replaced by the expression in the respective second element. This uses the same format as the SymPy subs() method. The order in which they are applied is simply their order in the list. The value of the conditions property of all states in inputs and gates in gates are automatically merged into the instance’s corresponding conditions property. Defaults to [].

Note

All states, gates, postselections, and measurement operators recorded in the instance must share the same dimensionality (i.e., the value of the dim property).

Note

The sum of the num_systems properties of the quantum states in inputs should match that of each of the gates in gates.

Examples

Listing 1 Bit-flip#

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit

# Input
input_state = VectorState(spec=[("a", [0]), ("b", [1])], label="ψ")

# Gate
NOT = Not()

# Circuit
bitflip = QuantumCircuit(inputs=[input_state], gates=[NOT])
bitflip.diagram(pad=(0, 0), sep=(1, 1), style="unicode")

# Output
output_state = bitflip.state(label="ψ'")

# Results
input_state.print()
output_state.print()

>>> bitflip.diagram(pad=(0, 0), sep=(1, 1), style="unicode")

>>> input_state.print()
|ψ⟩ = a|0⟩ + b|1⟩

>>> output_state.print()
|ψ'⟩ = b|0⟩ + a|1⟩

Listing 2 Arbitrary state generation#

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Rotation, Diagonal
from qhronology.quantum.circuits import QuantumCircuit

# Input
zero_state = VectorState(spec=[(1, [0])], label="0")

# Gates
R = Rotation(axis=1, angle="2*θ", symbols={"θ": {"real": True}}, label="R(2θ)")
P = Diagonal(
    entries={1: "φ + pi/2"},
    exponentiation=True,
    symbols={"φ": {"real": True}},
    label="P(φ + π/2)",
)

# Circuit
generator = QuantumCircuit(inputs=[zero_state], gates=[R, P])
generator.diagram(pad=(0, 0), sep=(1, 1), style="unicode")

# Output
arbitrary_state = generator.state(label="ψ")
arbitrary_state.simplify()

# Results
arbitrary_state.print()

>>> generator.diagram(pad=(0, 0), sep=(1, 1), style="unicode")

>>> arbitrary_state.print()
|ψ⟩ = cos(θ)|0⟩ + exp(I*φ)*sin(θ)|1⟩

Listing 3 CNOTs equivalent to SWAP#

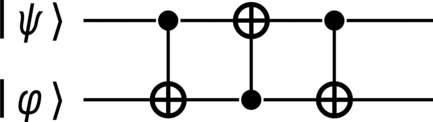
from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit

# Input
psi = VectorState(
    spec=[("a", [0]), ("b", [1])],
    conditions=[("a*conjugate(a) + b*conjugate(b)", 1)],
    label="ψ",
)
phi = VectorState(
    spec=[("c", [0]), ("d", [1])],
    conditions=[("c*conjugate(c) + d*conjugate(d)", 1)],
    label="φ",
)

# Gates
CN = Not(targets=[1], controls=[0])
NC = Not(targets=[0], controls=[1])

# Circuit
swapcnots = QuantumCircuit(inputs=[psi, phi], gates=[CN, NC, CN])
swapcnots.diagram(pad=(0, 0), sep=(1, 1), style="unicode")

# Output
print(repr(swapcnots.gate()))
upper = swapcnots.state(traces=[1], label="ψ'")
lower = swapcnots.state(traces=[0], label="φ'")
upper.kind = "pure"
lower.kind = "pure"
upper.simplify()
lower.simplify()

# Results
psi.print()
upper.print()
phi.print()
lower.print()

print(upper.distance(phi))
print(lower.distance(psi))

print(upper.fidelity(phi))
print(lower.fidelity(psi))

>>> swapcnots.diagram(pad=(0, 0), sep=(1, 1), style="unicode")

>>> psi.print()
|ψ⟩ = a|0⟩ + b|1⟩

>>> upper.print()
|ψ'⟩⟨ψ'| = c*conjugate(c)|0⟩⟨0| + c*conjugate(d)|0⟩⟨1| + d*conjugate(c)|1⟩⟨0| + d*conjugate(d)|1⟩⟨1|

>>> phi.print()
|φ⟩ = c|0⟩ + d|1⟩

>>> lower.print()
|φ'⟩⟨φ'| = a*conjugate(a)|0⟩⟨0| + a*conjugate(b)|0⟩⟨1| + b*conjugate(a)|1⟩⟨0| + b*conjugate(b)|1⟩⟨1|

>>> upper.distance(phi)
0

>>> lower.distance(psi)
0

>>> upper.fidelity(phi)
1

>>> lower.fidelity(psi)
1

Listing 4 Bell postselection#

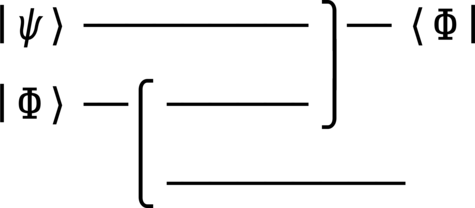
from qhronology.quantum.states import VectorState
from qhronology.quantum.circuits import QuantumCircuit

# Input
input_state = VectorState(
    spec=[("a", [0]), ("b", [1])],
    conditions=[("a*conjugate(a) + b*conjugate(b)", 1)],
    label="ψ",
)
bell = VectorState(spec=[(1, [0, 0]), (1, [1, 1])], norm=False, label="Φ")

# Circuit
postselection = QuantumCircuit(
    inputs=[input_state, bell], gates=[], postselections=[(bell, [0, 1])]
)
postselection.diagram(pad=(0, 0), sep=(4, 1), style="unicode")

# Output
output_state = postselection.state(label="ψ'")
input_state.print()
output_state.print()

>>> postselection.diagram(pad=(0, 0), sep=(4, 1), style="unicode")

>>> input_state.print()
|ψ⟩ = a|0⟩ + b|1⟩

>>> output_state.print()
|ψ'⟩ = a|0⟩ + b|1⟩

Listing 5 Fourier transform decomposition#

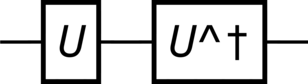
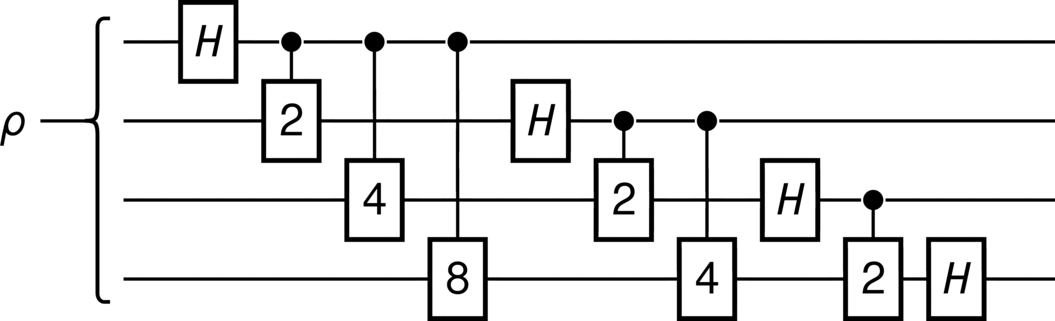
from qhronology.quantum.states import MatrixState
from qhronology.quantum.gates import Hadamard, Phase, Fourier
from qhronology.quantum.circuits import QuantumCircuit

import sympy as sp

size = 4  # Adjust the number of qudits
dim = 2  # Adjust the dimensionality of the Fourier transform

# Input
rho = sp.MatrixSymbol("ρ", dim**size, dim**size).as_mutable()
input_state = MatrixState(spec=rho, dim=dim, label="ρ")

# Gates
QFT = []
for i in range(0, size):
    count = size - i
    for j in range(0, count):
        if j == 0:
            QFT.append(Hadamard(targets=[i], dim=dim, num_systems=size))
        else:
            QFT.append(
                Phase(
                    targets=[i + j],
                    controls=[i],
                    exponent=sp.Rational(1, dim**j),
                    dim=dim,
                    num_systems=size,
                    label=f"{dim**j}",
                    family="GATE",
                )
            )

# Circuit
fourier = QuantumCircuit(inputs=[input_state], gates=QFT)
fourier.diagram(pad=(0, 0), sep=(0, 1), style="unicode")

# Output
print(repr(fourier.gate()))

>>> fourier.diagram(pad=(0, 0), sep=(0, 1), style="unicode")

Constructor argument properties#

property QuantumCircuit.inputs: list[QuantumState]#

An ordered list of QuantumState instances.

The total input state is the tensor product of these individual states in the order in which they appear in the list.

Each state’s symbols and conditions properties are merged into their counterparts in the instance upon their addition to the gates property.

property QuantumCircuit.gates: list[QuantumGate]#

An ordered list of QuantumGate instances.

The total gate is the product of these individual gates in the order in which they appear in the list.

Must all have the same num_systems property.

Each gate’s symbols and conditions properties are merged into their counterparts in the instance upon their addition to the gates property.

property QuantumCircuit.traces: list[int]#: The numerical indices of the subsystems to be traced over.

property QuantumCircuit.postselections: list[tuple[MutableDenseMatrix | ndarray | QuantumObject, int | list[int]]]#

A list of 2-tuples of vectors or matrix operators paired with the first (smallest) index of their postselection target systems.

Any symbols and conditions properties of each postselection are merged into their counterparts in the instance upon their addition to the postselections property.

property QuantumCircuit.symbols: dict[MatrixSymbol | MatrixElement | Symbol | str, dict[str, Any]]#

A dictionary in which the keys are individual symbols (contained within the object’s matrix representation) and the values are dictionaries of their respective SymPy keyword-argument assumptions (“predicates”). A full list of currently supported predicates, and their defaults, is as follows:

"algebraic": True
"commutative": True
"complex": True
"extended_negative": False
"extended_nonnegative": True
"extended_nonpositive": False
"extended_nonzero": True
"extended_positive": True
"extended_real": True
"finite": True
"hermitian": True
"imaginary": False
"infinite": False
"integer": True
"irrational": False
"negative": False
"noninteger": False
"nonnegative": True
"nonpositive": False
"nonzero": True
"positive": True
"rational": True
"real": True
"transcendental": False
"zero": False

property QuantumCircuit.conditions: list[tuple[Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str, Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str]]#: A list of \(2\)-tuples of conditions to be applied to the object’s matrix representation.

Read-only properties#

property QuantumCircuit.dim: int#: The dimensionality of the circuit. Calculated from its states and gates, and so all must have the same value.

property QuantumCircuit.systems: list[int]#: An ordered list of the numerical indices of the circuit’s systems.

property QuantumCircuit.systems_traces: list[int]#: The indices of the systems to be traced over.

property QuantumCircuit.systems_postselections: list[int]#: The indices of the systems to be postselected.

property QuantumCircuit.systems_removed: list[int]#: The indices of all of the systems targeted by the traces and postselections properties.

property QuantumCircuit.num_systems: int#: Alias for num_systems_gross.

property QuantumCircuit.num_systems_inputs: int#: The total number of systems spanned by the circuit’s input states.

property QuantumCircuit.num_systems_gates: int#: The total number of systems spanned by the circuit’s gates.

property QuantumCircuit.num_systems_gross: int#: The total number of systems spanned by the circuit’s states and gates prior to any system reduction (post-processing, i.e., traces and postselections]).

property QuantumCircuit.num_systems_net: int#: The total number of systems spanned by the circuit’s states and gates after any system reduction (post-processing, i.e., traces and postselections]).

property QuantumCircuit.num_systems_removed: int#: The total number of systems removed via system reduction (post-processing, i.e., traces and postselections]).

property QuantumCircuit.input_is_vector: bool#: Whether all states in inputs are vector states.

property QuantumCircuit.gate_is_linear: bool#: Whether all gates are linear (i.e., not measurement operations).

property QuantumCircuit.post_is_vector: bool#: Whether any traces or non-vector postselections exist in the circuit’s post-processing (trace and postselection) stage.

property QuantumCircuit.output_is_vector: bool#: Whether or not the output from the entire circuit is a vector state.

property QuantumCircuit.matrix: MutableDenseMatrix#: The matrix representation of the total output state prior to any post-processing (i.e., traces and postselections).

Methods#

Construct the composite input state of the quantum circuit as a QuantumState instance and return it.

This is computed as the tensor product of the individual gates in the order in which they appear in the inputs property. Is a vector state only when all of the component states are vectors.

Parameters:

conditions (list[tuple[num | sym | str, num | sym | str]]) – Algebraic conditions to be applied to the state. Defaults to the value of self.conditions.
simplify (bool) – Whether to perform algebraic simplification on the state. Defaults to False.
conjugate (bool) – Whether to perform Hermitian conjugation on the state. Defaults to False.
norm (bool | num | sym | str) – The value to which the state is normalized. If True, normalizes to a value of \(1\). If False, does not normalize. Defaults to False.
label (str) – The unformatted string used to represent the state in mathematical expressions. Must have a non-zero length. Defaults to "⊗".join([state.label for state in self.inputs]).
notation (str) – The formatted string used to represent the state in mathematical expressions. When not None, overrides the value passed to label. Must have a non-zero length. Not intended to be set by the user in most cases. Defaults to None.
debug (bool) – Whether to print the internal state (held in matrix) on change. Defaults to False.

Returns:

mat – The total input state as a QuantumState instance.

Construct the combined gate describing the total sequence of gates in the quantum circuit as a QuantumGate instance and return it.

This is computed as the matrix product of the individual gates in the reverse order in which they appear in the gates property.

Parameters:

conditions (list[tuple[num | sym | str, num | sym | str]]) – Algebraic conditions to be applied to the gate. Defaults to the value of self.conditions.
simplify (bool) – Whether to perform algebraic simplification on the gate. Defaults to False.
conjugate (bool) – Whether to perform Hermitian conjugation on the gate when it is called. Defaults to False.
exponent (num | sym | str) – A numerical or string representation of a scalar value to which gate’s operator (residing on targets) is exponentiated. Must be a non-negative integer. Defaults to 1.
label (str) – The unformatted string used to represent the gate in mathematical expressions. Defaults to "U".
notation (str) – The formatted string used to represent the gate in mathematical expressions. When not None, overrides the value passed to label. Not intended to be set by the user in most cases. Defaults to None.

Returns:

mat – The matrix or vector representation of the total gate sequence.

Note

This construction excludes measurement gates as they do not have a corresponding matrix representation.

Compute the matrix representation of the total output state of the circuit (including any post-processing, i.e., traces and postselections) and return it.

Parameters:

conditions (list[tuple[num | sym | str, num | sym | str]]) – Algebraic conditions to be applied to the state. Defaults to the value of self.conditions.
simplify (bool) – Whether to perform algebraic simplification on the state. Defaults to False.
conjugate (bool) – Whether to perform Hermitian conjugation on the state. Defaults to False.
postprocess (bool) – Whether to post-process the state (i.e., perform the circuit’s traces and postselections). Defaults to True.

Returns:

mat – The matrix representation of the (post-processed) output state.

Compute the total output state of the circuit (including any post-processing, i.e., traces and postselections) as a QuantumState instance and return it.

Parameters:

conditions (list[tuple[num | sym | str, num | sym | str]]) – Algebraic conditions to be applied to the state. Defaults to the value of self.conditions.
simplify (bool) – Whether to perform algebraic simplification on the state before committing it to the matrix property. Defaults to False.
conjugate (bool) – Whether to perform Hermitian conjugation on the state. Defaults to False.
norm (bool | num | sym | str) – The value to which the state is normalized. If True, normalizes to a value of \(1\). If False, does not normalize. Defaults to False.
label (str) – The unformatted string used to represent the state in mathematical expressions. Must have a non-zero length. Defaults to "ρ" (if form == "matrix") or "ψ" (if form == "vector").
notation (str) – The formatted string used to represent the state in mathematical expressions. When not None, overrides the value passed to label. Must have a non-zero length. Not intended to be set by the user in most cases. Defaults to None.
traces (list[int]) – A list of indices of the systems (relative to the entire circuit) on which to perform partial traces. Performed regardless of the value of postprocess. Defaults to [].
postprocess (bool) – Whether to post-process the state (i.e., perform the circuit’s traces and postselections). Defaults to True.
debug (bool) – Whether to print the internal state (held in matrix) on change. Defaults to False.

Returns:

QuantumState – The (post-processed) output state as a QuantumState instance.

Perform a quantum measurement on one or more systems (indicated in targets) of the circuit’s total output state. This occurs prior to any post-processing (i.e., traces and postselections).

This method has two main modes of operation:

When statistics is True, the (reduced) state (\(\op{\rho}\)) (residing on the systems indicated in targets) is measured and the set of resulting statistics is returned. This takes the form of an ordered list of values \(\{p_i\}_i\) associated with each given operator, where:
- \(p_i = \trace[\Kraus_i^\dagger \Kraus_i \op{\rho}]\) (measurement probabilities) when observable is False (operators is a list of Kraus operators or projectors \(\Kraus_i\))
- \(p_i = \trace[\Observable_i \op{\rho}]\) (expectation values) when observable is True (operators is a list of observables \(\Observable_i\))
When statistics is False, the (reduced) state (\(\op{\rho}\)) (residing on the systems indicated in targets) is measured and mutated it according to its predicted post-measurement form (i.e., the sum of all possible measurement outcomes). This yields the transformed states:
- When observable is False:
(305)#\[\op{\rho}^\prime = \sum_i \Kraus_i \op{\rho} \Kraus_i^\dagger.\]
- When observable is True:
(306)#\[\op{\rho}^\prime = \sum_i \trace[\Observable_i \op{\rho}] \Observable_i.\]

In the case where operators contains only a single item (\(\Kraus\)), and the current state (\(\ket{\psi}\)) is a vector form, the transformation of the state is in accordance with the rule

(307)#\[\ket{\psi^\prime} = \frac{\Kraus \ket{\psi}} {\sqrt{\bra{\psi} \Kraus^\dagger \Kraus \ket{\psi}}}\]

when observable is False. In all other mutation cases, the post-measurement state is a matrix, even if the pre-measurement state was a vector.

The items in the list operators can also be vectors (e.g., \(\ket{\xi_i}\)), in which case each is converted into its corresponding operator matrix representation (e.g., \(\ket{\xi_i}\bra{\xi_i}\)) prior to any measurements.

Parameters:

operators (list[mat | arr | QuantumObject]) – The operator(s) with which to perform the measurement. These would typically be a (complete) set of Kraus operators forming a POVM, a (complete) set of (orthogonal) projectors forming a PVM, or a set of observables constituting a complete basis for the relevant state space.
targets (int | list[int]) – The numerical indices of the system(s) to be measured. They must be consecutive, and their number must match the number of systems spanned by all given operators. Indexing begins at 0. All other systems are discarded (traced over) in the course of performing the measurement.
observable (bool) – Whether to treat the items in operators as observables (as opposed to Kraus operators or projectors). Defaults to False.
statistics (bool) – Whether to return a list of probabilities (True) or mutate the state into a post-measurement probabilistic sum of all outcomes (False). Defaults to False.

Returns:

list[num | sym] – A list of probabilities corresponding to each operator given in operators. Returned only if statistics is True.
QuantumState – A quantum state that takes the form of the post-measurement probabilistic sum of all outcomes of measurements corresponding to each operator given in operators. Returned only if statistics is False.

Print or return a diagram of the quantum circuit as a multiline string.

Parameters:

pad (tuple[int, int]) – A two-tuple describing the horizontal and vertical interior paddings between the content at the centre of each gate (e.g., label) and its outer edge (e.g., block border). Both integers must be non-negative. Defaults to (0, 0).
sep (tuple[int, int]) – A two-tuple describing the horizontal and vertical exterior separation distances between the edges of neighbouring gates. Both integers must be non-negative. Defaults to (1, 1).
uniform_spacing (bool) – Whether to uniformly space the gates horizontally such that the midpoint of each is equidistant from those of its neighbours. Defaults to False.
force_separation (bool) – Whether to force the horizontal gate separation to be exactly the value given in sep for all gates in the circuit. When not False, the value of uniform_spacing is ignored. Defaults to False.
style (str) – A string specifying the style for the circuit visualization to take. Can be any of "ascii", "unicode", or "unicode_alt". Defaults to "unicode".
return_string (bool) – Whether to return the assembled diagram as a multiline string. Defaults to False.

Returns:

None – Returned only if return_string is False.
str – The rendered circuit diagram. Returned only if return_string is True.

Note

The quality of the visualization depends greatly on the output’s configuration. For best results, the terminal should have a monospace font with good Unicode coverage.

Examples

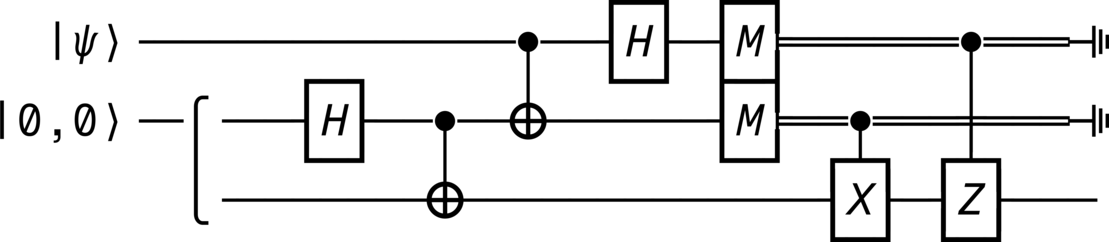
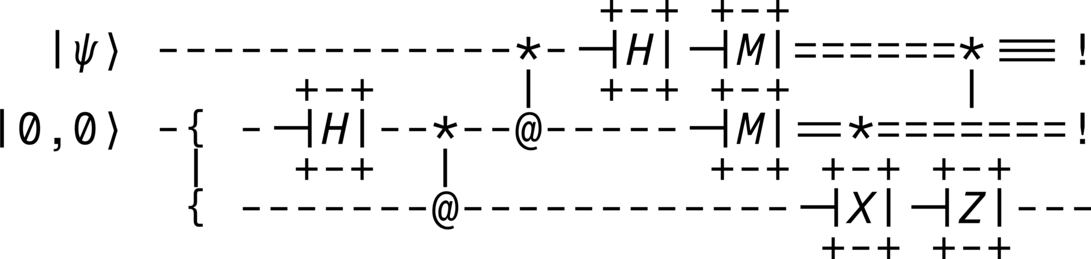
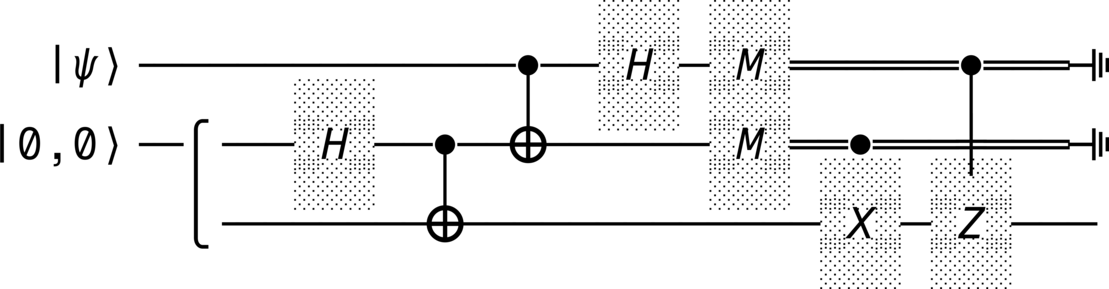
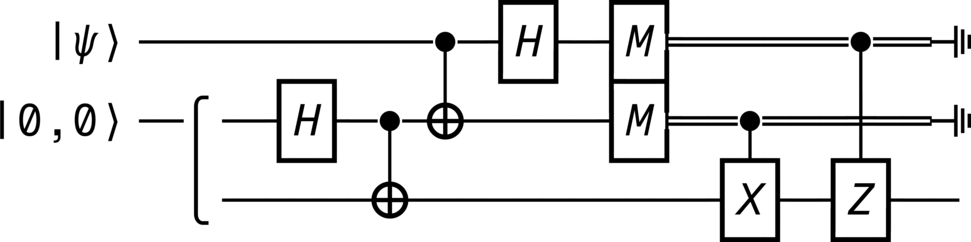
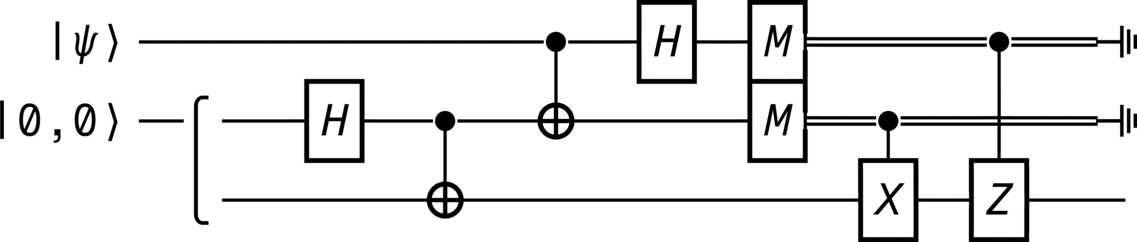
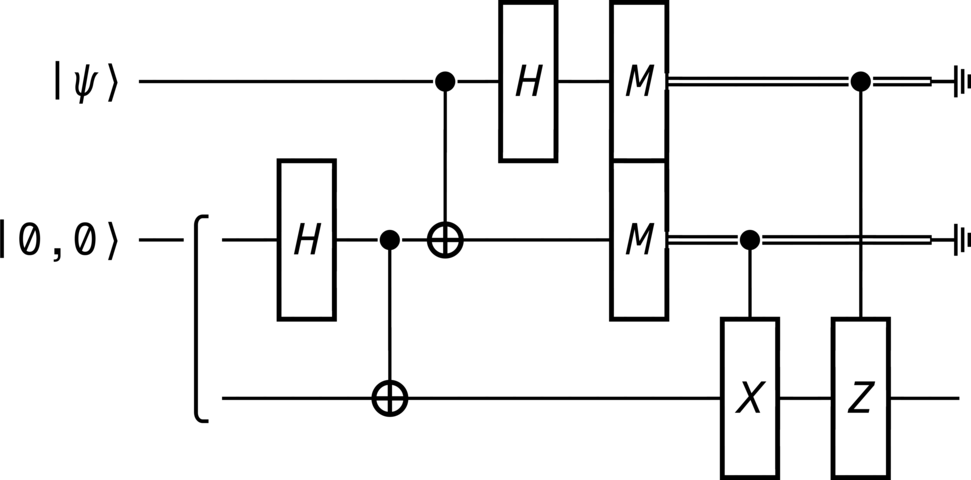
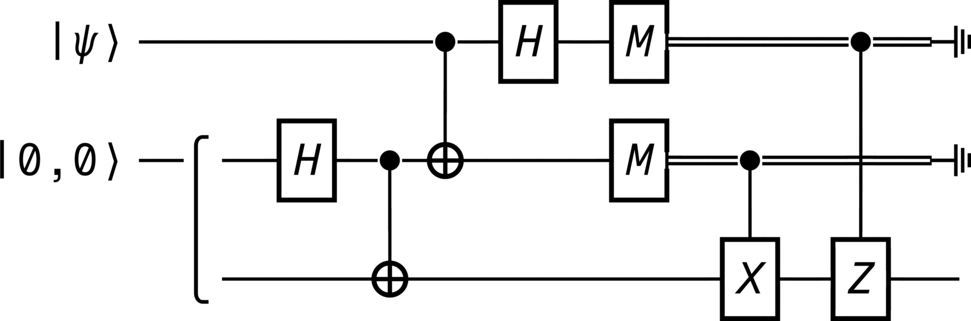
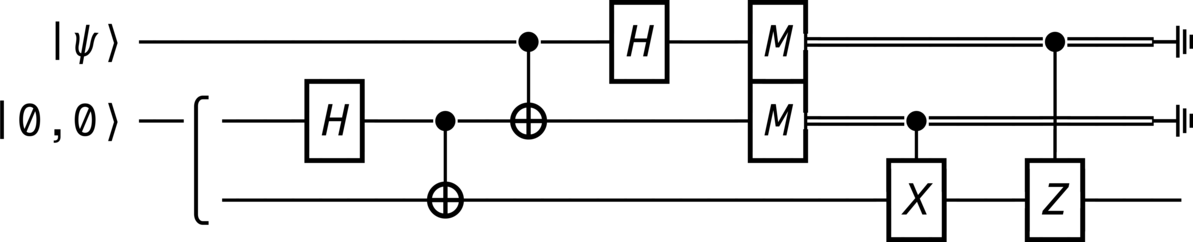
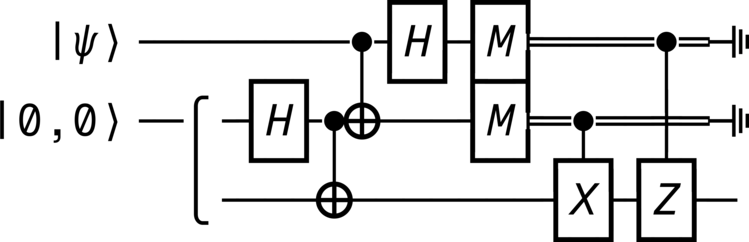
from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Hadamard, Not, Measurement, Pauli, GateInterleave
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.mechanics.matrices import ket

# Input
teleporting_state = VectorState(
    spec=[["a", "b"]],
    symbols={"a": {"complex": True}, "b": {"complex": True}},
    conditions=[("a*conjugate(a) + b*conjugate(b)", "1")],
    label="ψ",
)
zero_state = VectorState(spec=[(1, [0, 0])], label="0,0")

# Gates
IHI = Hadamard(targets=[1], num_systems=3)
ICN = Not(targets=[2], controls=[1], num_systems=3)
CNI = Not(targets=[1], controls=[0], num_systems=3)
HII = Hadamard(targets=[0], num_systems=3)
IMI = Measurement(
    operators=[ket(0), ket(1)], observable=False, targets=[1], num_systems=3
)
MII = Measurement(
    operators=[ket(0), ket(1)], observable=False, targets=[0], num_systems=3
)
MMI = GateInterleave(MII, IMI)
ICX = Pauli(index=1, targets=[2], controls=[1], num_systems=3)
CIZ = Pauli(index=3, targets=[2], controls=[0], num_systems=3)

# Circuit
circuit = QuantumCircuit(
    inputs=[teleporting_state, zero_state],
    gates=[IHI, ICN, CNI, HII, MMI, ICX, CIZ],
    traces=[0, 1],
)

>>> circuit.diagram(pad=(0, 0), sep=(1, 1), style="unicode")

>>> circuit.diagram(pad=(0, 0), sep=(1, 1), style="ascii")

>>> circuit.diagram(pad=(0, 0), sep=(1, 1), style="unicode_alt")

>>> circuit.diagram(pad=(0, 0), sep=(1, 1), force_separation=True, style="unicode")

>>> circuit.diagram(pad=(0, 0), sep=(1, 1), uniform_spacing=True, style="unicode")

>>> circuit.diagram(pad=(0, 1), sep=(1, 1), force_separation=True, style="unicode")

>>> circuit.diagram(pad=(1, 0), sep=(1, 1), force_separation=True, style="unicode")

>>> circuit.diagram(pad=(0, 0), sep=(1, 2), force_separation=True, style="unicode")

>>> circuit.diagram(pad=(0, 0), sep=(2, 1), force_separation=True, style="unicode")

>>> circuit.diagram(pad=(0, 0), sep=(0, 1), force_separation=True, style="unicode")