Prescriptions#

In Qhronology, quantum circuit models of closed timelike curves (CTCs) are created as instances of the QuantumCTC class:

from qhronology.quantum.prescriptions import QuantumCTC

This provides almost identical functionality as the QuantumCircuit class (from which it is derived), differing only in the addition of the systems_respecting and systems_violating properties.

Built upon the QuantumCTC class are the various theoretical models (prescriptions) of quantum time travel. Qhronology currently implements two such prescriptions: Deutsch’s model (D-CTCs) and postselected teleportation (P-CTCs):

from qhronology.quantum.prescriptions import DCTC, PCTC

Due to their close relationship, instances of the QuantumCTC class can be created directly from instances of the QuantumCircuit class. This is achieved by way of the circuit argument in the QuantumCTC constructor, whereby all attributes of the given QuantumCircuit instance are copied (deeply) to the QuantumCTC instance during initialization. Importantly, this enables the various subclasses, such as DCTC and PCTC, to be instantiated entirely using a single QuantumCTC instance, thereby reducing duplication (of arguments) when one wishes to study multiple prescriptions of the same CTC circuit.

Main class#

Please note that the documentation of this class includes only properties and methods that are either new or modified from its base class QuantumCircuit.

class QuantumCTC(

*args,

circuit: QuantumCircuit | None = None,

systems_respecting: list[int] | None = None,

systems_violating: list[int] | None = None,

**kwargs,

)[source]#

Bases: QuantumCircuit

A class for creating quantum circuit models of quantum interactions near closed timelike curves and storing their metadata.

This is built upon the QuantumCircuit class, and so inherits all of its attributes, properties, and methods.

Instances provide complete descriptions of quantum circuits involving antichronological time travel. The class however does not possess any ability to compute the output state (e.g., resolve temporal paradoxes) of the circuit; this is functionality that is associated with the specific prescriptions of quantum time travel, and such prescriptions are implemented as subclasses.

Parameters:

*args – Variable length argument list, passed directly to the constructor __init__ of the superclass QuantumCircuit.
circuit (QuantumCircuit) – An instance of the QuantumCircuit class. The values of its attributes override any other values specified in *args and **kwargs. Defaults to None.
systems_respecting (int | list[int]) – The numerical indices of the chronology-respecting (CR) subsystems. Defaults to [].
systems_violating (int | list[int]) – The numerical indices of the chronology-violating (CV) subsystems. Defaults to [].
**kwargs – Arbitrary keyword arguments, passed directly to the constructor __init__ of the superclass QuantumCircuit.

Note

The lists of indices specified in systems_respecting and systems_violating must both be contiguous. Additionally, the circuit’s inputs (inputs) are treated as one contiguous total state, with the indices of its subsystems exactly matching those specified in systems_respecting.

Note

It is best practice to specify only one of either systems_violating or systems_violating, never both. The properties associated with both of these constructor arguments automatically ensure that they are always complementary (with respect to the entire system space), and so only one needs to be specified.

Note

The circuit argument can be used to merge the value of every attribute from a pre-existing QuantumCircuit instance into the QuantumCTC instance. Any such mergers override the values of the attributes associated with the other arguments specified in the constructor. It is best practice to specify either of:

only circuit and one of either systems_respecting or systems_violating
*args and **kwargs (like a typical initialization of a QuantumCircuit instance) without specifying circuit

Note

The total interaction between the CR and CV systems is expected to be unitary, and so the sequence of gates in gates cannot contain any non-unitary gates (e.g., measurement operations).

Note

Post-processing (e.g., traces and postselections) cannot be performed on any chronology-violating (CV) systems (i.e., those corresponding to indices specified in systems_violating).

Examples

Listing 7 SWAP interaction with a CTC#

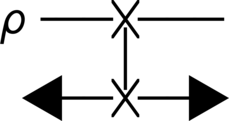
from qhronology.quantum.states import MixedState
from qhronology.quantum.gates import Swap, Pauli
from qhronology.quantum.prescriptions import QuantumCTC, DCTC, PCTC

import sympy as sp

# Input
rho = sp.MatrixSymbol("ρ", 2, 2).as_mutable()
input_state = MixedState(
    spec=rho,
    conditions=[(rho[1, 1], 1 - rho[0, 0])],
    label="ρ",
)

# Gate
S = Swap(targets=[0, 1], num_systems=2)
I = Pauli(index=0, targets=[0, 1], num_systems=2)

# CTC
SWAP = QuantumCTC([input_state], [S], systems_respecting=[0])
SWAP.diagram()

# Output
# D-CTCs
SWAP_DCTC = DCTC(circuit=SWAP)
SWAP_DCTC_respecting = SWAP_DCTC.state_respecting(norm=False, label="ρ_D")
SWAP_DCTC_violating = SWAP_DCTC.state_violating(norm=False, label="τ_D")
SWAP_DCTC_respecting.conditions = [(1 - rho[0, 0], rho[1, 1])]
SWAP_DCTC_respecting.simplify()
SWAP_DCTC_violating.conditions = [(1 - rho[0, 0], rho[1, 1])]

# P-CTCs
SWAP_PCTC = PCTC(circuit=SWAP)
SWAP_PCTC_respecting = SWAP_PCTC.state_respecting(norm=False, label="ρ_P")
SWAP_PCTC_violating = SWAP_PCTC.state_violating(norm=False, label="τ_P")
SWAP_PCTC_respecting.conditions = [(1 - rho[0, 0], rho[1, 1])]
SWAP_PCTC_violating.conditions = [(1 - rho[0, 0], rho[1, 1])]

SWAP_PCTC_respecting.simplify()
SWAP_PCTC_violating.simplify()

# Results
SWAP_DCTC_respecting.print()
SWAP_DCTC_violating.print()
SWAP_PCTC_respecting.print()
SWAP_PCTC_violating.print()

>>> SWAP.diagram()

>>> SWAP_DCTC_respecting.print()
ρ_D = ρ[0, 0]|0⟩⟨0| + ρ[0, 1]|0⟩⟨1| + ρ[1, 0]|1⟩⟨0| + ρ[1, 1]|1⟩⟨1|

>>> SWAP_DCTC_violating.print()
τ_D = ρ[0, 0]|0⟩⟨0| + ρ[0, 1]|0⟩⟨1| + ρ[1, 0]|1⟩⟨0| + ρ[1, 1]|1⟩⟨1|

>>> SWAP_PCTC_respecting.print()
ρ_P = ρ[0, 0]|0⟩⟨0| + ρ[0, 1]|0⟩⟨1| + ρ[1, 0]|1⟩⟨0| + ρ[1, 1]|1⟩⟨1|

>>> SWAP_PCTC_violating.print()
τ_P = ρ[0, 0]|0⟩⟨0| + ρ[0, 1]|0⟩⟨1| + ρ[1, 0]|1⟩⟨0| + ρ[1, 1]|1⟩⟨1|

Listing 8 CNOT interaction with a CTC#

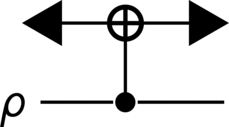
from qhronology.quantum.states import MixedState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.quantum.prescriptions import QuantumCTC, DCTC, PCTC

import sympy as sp

# Input
rho = sp.MatrixSymbol("ρ", 2, 2).as_mutable()
input_state = MixedState(spec=rho, conditions=[(rho[1, 1], 1 - rho[0, 0])], label="ρ")

# Gate
CN = Not(targets=[0], controls=[1], num_systems=2)

# CTC
CNOT = QuantumCircuit(inputs=[input_state], gates=[CN])
CNOT = QuantumCTC(circuit=CNOT, systems_respecting=[1])
CNOT.diagram()

# Output
# D-CTCs
CNOT_DCTC = DCTC(circuit=CNOT)
CNOT_DCTC_respecting = CNOT_DCTC.state_respecting(norm=False, label="ρ_D")
CNOT_DCTC_violating = CNOT_DCTC.state_violating(norm=False, label="τ_D")
CNOT_DCTC_respecting.conditions = [(1 - rho[0, 0], rho[1, 1])]

# P-CTCs
CNOT_PCTC = PCTC(circuit=CNOT)
CNOT_PCTC_respecting = CNOT_PCTC.state_respecting(norm=True, label="ρ_P")
CNOT_PCTC_violating = CNOT_PCTC.state_violating(norm=False, label="τ_P")

# Results
CNOT_DCTC_respecting.print()
CNOT_DCTC_violating.print()
CNOT_PCTC_respecting.print()
CNOT_PCTC_violating.print()

>>> CNOT.diagram()

>>> CNOT_DCTC_respecting.print()
ρ_D = ρ[0, 0]|0⟩⟨0| + 2*g*ρ[0, 1]|0⟩⟨1| + 2*g*ρ[1, 0]|1⟩⟨0| + ρ[1, 1]|1⟩⟨1|

>>> CNOT_DCTC_violating.print()
τ_D = 1/2|0⟩⟨0| + g|0⟩⟨1| + g|1⟩⟨0| + 1/2|1⟩⟨1|

>>> CNOT_PCTC_respecting.print()
ρ_P = |0⟩⟨0|

>>> CNOT_PCTC_violating.print()
τ_P = 1/2|0⟩⟨0| + 1/2|1⟩⟨1|

Constructor argument properties#

property QuantumCTC.systems_respecting: list[int]#: The numerical indices of the chronology-respecting (CR) subsystems.

property QuantumCTC.systems_violating: list[int]#: The numerical indices of the chronology-violating (CV) subsystems.

Methods#

Construct the composite chronology-respecting (CR) input state of the closed timelike curve as a QuantumState instance and return it.

This is computed as the tensor product of the individual gates in the order in which they appear in the inputs property. Is a vector state only when all of the component states are vectors.

Parameters:

conditions (list[tuple[num | sym | str, num | sym | str]]) – Algebraic conditions to be applied to the state. If False, does not substitute the conditions. Defaults to the value of self.conditions.
simplify (bool) – Whether to perform algebraic simplification on the state. Defaults to False.
conjugate (bool) – Whether to perform Hermitian conjugation on the state. Defaults to False.
norm (bool | num | sym | str) – The value to which the state is normalized. If True, normalizes to a value of \(1\). If False, does not normalize. Defaults to False.
label (str) – The unformatted string used to represent the state in mathematical expressions. Must have a non-zero length. Defaults to "⊗".join([state.label for state in self.inputs]).
notation (str) – The formatted string used to represent the state in mathematical expressions. When not None, overrides the value passed to label. Must have a non-zero length. Not intended to be set by the user in most cases. Defaults to None.
debug (bool) – Whether to print the internal state (held in matrix) on change. Defaults to False.

Returns:

mat – The total input state as a QuantumState instance.

Print or return a diagram of the quantum circuit as a multiline string.

Parameters:

pad (tuple[int, int]) – A two-tuple describing the horizontal and vertical interior paddings between the content at the centre of each gate (e.g., label) and its outer edge (e.g., block border). Both integers must be non-negative. Defaults to (0, 0).
sep (tuple[int, int]) – A two-tuple describing the horizontal and vertical exterior separation distances between the edges of neighbouring gates. Both integers must be non-negative. Defaults to (1, 1).
uniform_spacing (bool) – Whether to uniformly space the gates horizontally such that the midpoint of each is equidistant from those of its neighbours. Defaults to False.
force_separation (bool) – Whether to force the horizontal gate separation to be exactly the value given in sep for all gates in the circuit. When not False, the value of uniform_spacing is ignored. Defaults to False.
style (str) – A string specifying the style for the circuit visualization to take. Can be any of "ascii", "unicode", or "unicode_alt". Defaults to "unicode".
return_string (bool) – Whether to return the assembled diagram as a multiline string. Defaults to False.

Returns:

None – Returned only if return_string is False.
str – The rendered circuit diagram. Returned only if return_string is True.

Note

The quality of the visualization depends greatly on the output’s configuration. For best results, the terminal should have a monospace font with good Unicode coverage.

Examples

Please see the examples of the QuantumCTC class itself. For advanced usage examples, see the corresponding diagram() method of the QuantumCircuit class.

Subclasses#

Please note that the documentation of these subclasses includes only properties and methods that are either new or modified from the base class QuantumCTC.

D-CTCs#

Deutsch’s prescription (D-CTCs)
- Functions
- Class

P-CTCs#

Postselected teleportation (P-CTCs)
- Functions
- Class