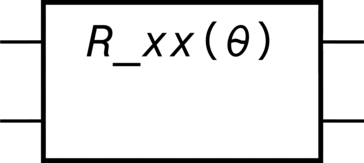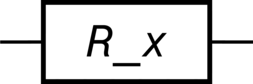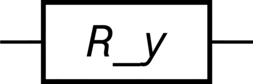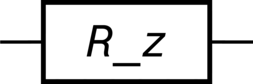Gates#
Quantum logic gates provide the building blocks for describing quantum operations that are usually (unitary) interactions between two or more (sub)systems, or (linear) transformations of any number of systems. In Qhronology, they are constructed as instances of the QuantumGate base class,
from qhronology.quantum.gates import QuantumGate
and its derivatives (subclasses),
from qhronology.quantum.gates import Pauli, GellMann, Rotation, Phase, Diagonal, Swap, Summation, Not, Hadamard, Fourier, Measurement
These represent a distinct vertical “slice” in the quantum circuit picturalism, and so include information about the locations of both control and anticontrol nodes, in addition to the presence of any empty wires. They also possess other metadata associated with the gate such as any parameter values, symbolic assumptions, and algebraic conditions.
Facilities to combine gates together are also provided by the package and take two forms: “interleaved” compositions via the GateInterleave class, and “stacked” compositions via the GateStack class:
from qhronology.quantum.gates import GateInterleave, GateStack
Both of these classes concern the creation of more complex spatial (“vertical”) gate structures. Temporal (“horizontal”) compositions (i.e., gates wired in serial) as single object instances on the other hand are not supported as this is achievable simply by combining the individual components sequentially in a circuit.
Main class#
- class QuantumGate(
- spec: MutableDenseMatrix | ndarray | list[list[Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str]] | None,
- targets: list[int] | None = None,
- controls: list[int] | None = None,
- anticontrols: list[int] | None = None,
- num_systems: int | None = None,
- dim: int | None = None,
- symbols: dict | None = None,
- conditions: list[tuple[Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str, Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str]] | None = None,
- conjugate: bool | None = None,
- exponent: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- coefficient: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- label: str | None = None,
- notation: str | None = None,
- family: str | None = None,
Bases:
QuantumObjectA class for creating quantum gates and storing their metadata.
This class forms the base upon which all quantum gates are built. Instances of this base class and its derivatives (subclasses) provide complete descriptions of quantum gates. This means that they describe a complete vertical column (or “slice”) in the quantum circuitry picturalism, including control nodes, anticontrol nodes, empty wires, and the (unitary) gate operator itself. The details of any algebraic symbols, mathematical conditions, and visualization labels are also recorded. Note that, unlike the internal matrix representations contained within instances of the
QuantumStateclass (and its derivatives), the matrix representations of subclass instances ofQuantumGateare not mutable.- Parameters:
spec (mat | arr | list[list[num | sym | str]]) –
The specification of the quantum gate’s matrix representation in a standard
dim-dimensional basis. Can be one of:a SymPy matrix (
mat)a NumPy array (
arr)a list of lists of numerical, symbolic, or string expressions that collectively specify a matrix (
list[list[num | sym | str]])
Defaults to the single-system
dim-dimensional Identity operator.targets (list[int]) – The numerical indices of the subsystems on which the gate elements reside. Defaults to
[0](ifnum_systemsisNone) or[i for i in range(num_systems)](ifnum_systemsis notNone).controls (list[int]) – The numerical indices of the subsystems on which control nodes reside. Defaults to
[].anticontrols (list[int]) – The numerical indices of the subsystems on which anticontrol nodes reside. Defaults to
[].num_systems (int) – The (total) number of systems which the gate spans. Must be a non-negative integer. Defaults to
max(targets + controls + anticontrols + [count_systems(sp.Matrix(spec), dim)]) + 1.dim (int) – The dimensionality of the quantum gate’s Hilbert space. Must be a non-negative integer. Defaults to
2.symbols (dict[sym | str, dict[str, Any]]) – A dictionary in which the keys are individual symbols (usually found within the gate specification
spec) and the values are dictionaries of their respective SymPy keyword-argumentassumptions. Defaults to{}.conditions (list[tuple[num | sym | str, num | sym | str]]) – A list of \(2\)-tuples of conditions to be applied to the gate. All instances of the expression in each tuple’s first element are replaced by the expression in the respective second element. This uses the same format as the SymPy
subs()method. The order in which they are applied is simply their order in the list. Defaults to[].conjugate (bool) – Whether to perform Hermitian conjugation on the gate when it is called. Defaults to
False.exponent (num | sym | str) – A numerical or string representation of a scalar value to which gate’s operator (residing on
targets) is exponentiated. Must be a non-negative integer. Useful for computing powers of gates (such as PSWAP), but is only guaranteed to return a valid power of a gate if its corresponding matrix representation (e.g., \(\op{A}\)) is involutory (i.e., \(\op{A}^2 = \Identity\)). Defaults to1.coefficient (num | sym | str) – A numerical or string representation of a scalar value by which the gate’s matrix (occupying
targets) is multiplied. Performed after exponentiation. Useful for multiplying the gate by a phase factor. Defaults to1.label (str) – The unformatted string used to represent the gate in mathematical expressions. Defaults to
"U".notation (str) – The formatted string used to represent the gate in mathematical expressions. When not
None, overrides the value passed tolabel. Not intended to be set by the user in most cases. Defaults toNone.family (str) – A string expressing the kind of block element for which the gate is to be visualized. Not intended to be set by the user. Defaults to
"GATE".
Note
The indices specified in
targets,controls, andanticontrolsmust be distinct.Examples
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> U = QuantumGate(spec=unitary, label="U") >>> U.output() Matrix([ [U[0, 0], U[0, 1]], [U[1, 0], U[1, 1]]]) >>> U.diagram()
>>> unitary = sp.MatrixSymbol("U", 3, 3).as_mutable() >>> U3 = QuantumGate(spec=unitary, label="U", dim=3) >>> U3.output() Matrix([ [U[0, 0], U[0, 1], U[0, 2]], [U[1, 0], U[1, 1], U[1, 2]], [U[2, 0], U[2, 1], U[2, 2]]]) >>> U3.diagram()
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> UI = QuantumGate(spec=unitary, targets=[0], num_systems=2, label="U") >>> UI.output() Matrix([ [U[0, 0], 0, U[0, 1], 0], [ 0, U[0, 0], 0, U[0, 1]], [U[1, 0], 0, U[1, 1], 0], [ 0, U[1, 0], 0, U[1, 1]]]) >>> UI.diagram()
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> IU = QuantumGate(spec=unitary, targets=[1], num_systems=2, label="U") >>> IU.output() Matrix([ [U[0, 0], U[0, 1], 0, 0], [U[1, 0], U[1, 1], 0, 0], [ 0, 0, U[0, 0], U[0, 1]], [ 0, 0, U[1, 0], U[1, 1]]]) >>> IU.diagram()
>>> unitary = sp.MatrixSymbol("U", 4, 4).as_mutable() >>> UU = QuantumGate(spec=unitary, targets=[0, 1], num_systems=2, label="U") >>> UU.output() Matrix([ [U[0, 0], U[0, 1], U[0, 2], U[0, 3]], [U[1, 0], U[1, 1], U[1, 2], U[1, 3]], [U[2, 0], U[2, 1], U[2, 2], U[2, 3]], [U[3, 0], U[3, 1], U[3, 2], U[3, 3]]]) >>> UU.diagram()
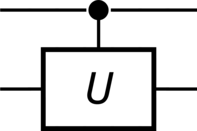
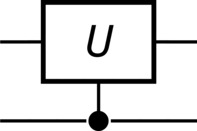
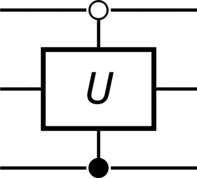
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> CU = QuantumGate(spec=unitary, targets=[1], controls=[0], label="U") >>> CU.output() Matrix([ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, U[0, 0], U[0, 1]], [0, 0, U[1, 0], U[1, 1]]]) >>> CU.diagram()
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> UC = QuantumGate(spec=unitary, targets=[0], controls=[1], label="U") >>> UC.output() Matrix([ [1, 0, 0, 0], [0, U[0, 0], 0, U[0, 1]], [0, 0, 1, 0], [0, U[1, 0], 0, U[1, 1]]]) >>> UC.diagram()
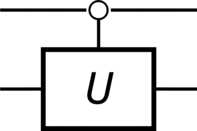
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> AU = QuantumGate(spec=unitary, targets=[1], anticontrols=[0], label="U") >>> AU.output() Matrix([ [U[0, 0], U[0, 1], 0, 0], [U[1, 0], U[1, 1], 0, 0], [ 0, 0, 1, 0], [ 0, 0, 0, 1]]) >>> AU.diagram()
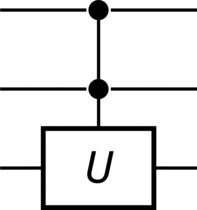
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> CCU = QuantumGate(spec=unitary, targets=[2], controls=[0, 1], label="U") >>> CCU.output() Matrix([ [1, 0, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, U[0, 0], U[0, 1]], [0, 0, 0, 0, 0, 0, U[1, 0], U[1, 1]]]) >>> CCU.diagram()
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> AUC = QuantumGate(spec=unitary, targets=[1], controls=[2], anticontrols=[0], label="U") >>> AUC.output() Matrix([ [1, 0, 0, 0, 0, 0, 0, 0], [0, U[0, 0], 0, U[0, 1], 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0], [0, U[1, 0], 0, U[1, 1], 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 0, 0, 1]]) >>> AUC.diagram()
Constructor argument properties#
- property QuantumGate.spec: MutableDenseMatrix | ndarray | list[list[Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str]]#
The matrix representation of the quantum gate’s operator. Provides a complete description of the operator in a standard
dim-dimensional basis.
- property QuantumGate.targets: list[int]#
The numerical indices of the subsystems on which the gate elements reside.
- property QuantumGate.controls: list[int]#
The numerical indices of the subsystems on which control nodes reside.
For example, a controlled-\(\Unitary\) gate in \(\Dimension\) dimensions takes the form
(288)#\[\begin{split}\begin{aligned} \Control^{0} \Unitary^{1} &= \sum\limits_{k=0}^{\Dimension - 1} \ket{k}\bra{k}\otimes\Unitary^{k} \\ &= \ket{0}\bra{0}\otimes\Identity + \ket{1}\bra{1}\otimes\Unitary + \ket{2}\bra{2}\otimes\Unitary^{2} + \ldots + \ket{\Dimension - 1}\bra{\Dimension - 1}\otimes\Unitary^{\Dimension - 1} \end{aligned}\end{split}\]
- property QuantumGate.anticontrols: list[int]#
The numerical indices of the subsystems on which anticontrol nodes reside.
For example, an anticontrolled-\(\Unitary\) gate in \(\Dimension\) dimensions takes the form
(289)#\[\begin{split}\begin{aligned} \Anticontrol^{0} \Unitary^{1} &= \sum\limits_{k=0}^{\Dimension - 1} \ket{k}\bra{k}\otimes\Unitary^{\Dimension - 1 - k} \\ &= \ket{0}\bra{0}\otimes\Unitary^{\Dimension - 1} + \ket{1}\bra{1}\otimes\Unitary^{\Dimension - 2} + \ket{2}\bra{2}\otimes\Unitary^{\Dimension - 3} + \ldots + \ket{\Dimension - 1}\bra{\Dimension - 1}\otimes\Identity \end{aligned}\end{split}\]
- property QuantumGate.num_systems: int#
The number of systems that the object spans. Must be a non-negative integer. Should not be set for states.
- property QuantumGate.dim: int#
The dimensionality of the quantum object. Must be a non-negative integer.
- property QuantumGate.symbols: dict[MatrixSymbol | MatrixElement | Symbol | str, dict[str, Any]]#
A dictionary in which the keys are individual symbols (contained within the object’s matrix representation) and the values are dictionaries of their respective SymPy keyword-argument
assumptions(“predicates”). A full list of currently supported predicates, and their defaults, is as follows:"algebraic":True"commutative":True"complex":True"extended_negative":False"extended_nonnegative":True"extended_nonpositive":False"extended_nonzero":True"extended_positive":True"extended_real":True"finite":True"hermitian":True"imaginary":False"infinite":False"integer":True"irrational":False"negative":False"noninteger":False"nonnegative":True"nonpositive":False"nonzero":True"positive":True"rational":True"real":True"transcendental":False"zero":False
- property QuantumGate.conditions: list[tuple[Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str, Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str]]#
A list of \(2\)-tuples of conditions to be applied to the object’s matrix representation.
- property QuantumGate.conjugate: bool#
Whether to perform Hermitian conjugation on the object when it is called.
- property QuantumGate.exponent: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str#
A numerical or string representation of a scalar value specifying the value to which the gate’s matrix representation is exponentiated. Is guaranteed to produce valid powers only for involutory matrices.
For an involutory matrix \(\op{A}\), that is \(\op{A}^2 = \Identity\) (where \(\Identity\) is the identity matrix), we have the identity,
(290)#\[\exp[\eye x \op{A}] = \cos(x)\Identity + \eye\sin(x)\op{A},\]for any \(x \in \Complexes\). In the case of \(x = -\frac{\pi}{2}\), this becomes
(291)#\[\exp\Bigl[-\eye\frac{\pi}{2}\op{A}\Bigr] = -\eye\op{A},\]which can be rearranged to give
(292)#\[\begin{split}\begin{aligned} \op{A} &= \eye \exp\Bigl[-\eye\frac{\pi}{2}\op{A}\Bigr] \\ &= \exp\Bigl[\eye\frac{\pi}{2}\Bigr] \cdot \exp\Bigl[-\eye\frac{\pi}{2}\op{A}\Bigr]. \end{aligned}\end{split}\]Simply taking this expression to an arbitrary power \(p \in \mathbb{C}\) thus yields the identity
(293)#\[\begin{split}\begin{aligned} \op{A}^p &= \exp\Bigl[\eye\frac{\pi}{2} p\Bigr] \cdot \exp\Bigl[-\eye\frac{\pi}{2} p \op{A}\Bigr] \\ &= \exp\Bigl[\eye\frac{\pi}{2} p\Bigr] \Bigl[\cos\Bigl(\frac{\pi}{2} p\Bigr) \Identity - \eye \sin\Bigl(\frac{\pi}{2} p\Bigr) \op{A}\Bigr] \\ &= \frac{1 + \e^{\eye \pi p}}{2} \Identity + \frac{1 - \e^{\eye \pi p}}{2} \op{A}. \end{aligned}\end{split}\]
- property QuantumGate.coefficient: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str#
A numerical or string representation of a scalar value by which the gate’s matrix (occupying
targets) is multiplied.
- property QuantumGate.label: str#
The unformatted string used to represent the object in mathematical expressions. Must have a non-zero length.
- property QuantumGate.notation: str#
The formatted string used to represent the object in mathematical expressions. When set, overrides the value of the
labelproperty. Must have a non-zero length. Not intended to be set by the user in most cases.
- property QuantumGate.family: str#
The code of the block element that the object is to be visualized as. Not intended to be set by the user.
Read-only properties#
- property QuantumGate.systems: list[int]#
Read-only property containing an ordered list of the numerical indices of the object’s systems.
- property QuantumGate.matrix: MutableDenseMatrix#
The matrix representation of the total gate across all of its systems.
Methods#
- QuantumGate.output(
- conditions: list[tuple[Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str, Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str]] | None = None,
- simplify: bool | None = None,
- conjugate: bool | None = None,
- exponent: bool | Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- coefficient: bool | Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
Construct the gate and return its matrix representation.
- Parameters:
conditions (list[tuple[num | sym | str, num | sym | str]]) – Algebraic conditions to be applied to the gate. Defaults to the value of
self.conditions.simplify (bool) – Whether to perform algebraic simplification on the gate. Defaults to
False.conjugate (bool) – Whether to perform Hermitian conjugation on the gate. If
False, does not conjugate. Defaults to the value ofself.conjugate.exponent (bool | num | sym | str) – The scalar value by which the gate’s matrix representation is exponentiated. If
False, does not exponentiate. Defaults to the value ofself.exponent.coefficient (num | sym | str) – The scalar value by which the gate’s matrix representation is multiplied. If
False, does not multiply the gate by the coefficient. Defaults to the value ofself.coefficient.
- Returns:
mat – The constructed quantum gate.
- QuantumGate.print(
- delimiter: str | None = None,
- product: bool | None = None,
- return_string: bool | None = None,
Print or return a mathematical expression of the quantum object as a string.
- Parameters:
delimiter (str) – A string containing the character(s) with which to delimit (i.e., separate) the values in the ket and/or bra terms in the mathematical expression. Defaults to
",".product (bool) – Whether to represent the mathematical expression using tensor products. Only applies if the object is a multipartite composition. Defaults to
False.return_string (bool) – Whether to return the mathematical expression as a string. Defaults to
False.
- Returns:
None – Returned only if
return_stringisFalse.str – The constructed mathematical expression. Returned only if
return_stringisTrue.
Examples
>>> unitary = sp.MatrixSymbol("U", 2, 2).as_mutable() >>> U = QuantumGate(spec=unitary, label="U", dim=2) >>> U.output() Matrix([ [U[0, 0], U[0, 1]], [U[1, 0], U[1, 1]]]) >>> U.print() U = U[0, 0]|0⟩⟨0| + U[0, 1]|0⟩⟨1| + U[1, 0]|1⟩⟨0| + U[1, 1]|1⟩⟨1|
>>> unitary = sp.MatrixSymbol("U", 4, 4).as_mutable() >>> UU = QuantumGate(spec=unitary, label="UU", dim=2, targets = [0,1]) >>> UU.output() Matrix([ [U[0, 0], U[0, 1], U[0, 2], U[0, 3]], [U[1, 0], U[1, 1], U[1, 2], U[1, 3]], [U[2, 0], U[2, 1], U[2, 2], U[2, 3]], [U[3, 0], U[3, 1], U[3, 2], U[3, 3]]]) >>> UU.print() UU = U[0, 0]|0,0⟩⟨0,0| + U[0, 1]|0,0⟩⟨0,1| + U[0, 2]|0,0⟩⟨1,0| + U[0, 3]|0,0⟩⟨1,1| + U[1, 0]|0,1⟩⟨0,0| + U[1, 1]|0,1⟩⟨0,1| + U[1, 2]|0,1⟩⟨1,0| + U[1, 3]|0,1⟩⟨1,1| + U[2, 0]|1,0⟩⟨0,0| + U[2, 1]|1,0⟩⟨0,1| + U[2, 2]|1,0⟩⟨1,0| + U[2, 3]|1,0⟩⟨1,1| + U[3, 0]|1,1⟩⟨0,0| + U[3, 1]|1,1⟩⟨0,1| + U[3, 2]|1,1⟩⟨1,0| + U[3, 3]|1,1⟩⟨1,1| >>> UU.print(product=True) UU = U[0, 0]|0⟩⟨0|⊗|0⟩⟨0| + U[0, 1]|0⟩⟨0|⊗|0⟩⟨1| + U[0, 2]|0⟩⟨1|⊗|0⟩⟨0| + U[0, 3]|0⟩⟨1|⊗|0⟩⟨1| + U[1, 0]|0⟩⟨0|⊗|1⟩⟨0| + U[1, 1]|0⟩⟨0|⊗|1⟩⟨1| + U[1, 2]|0⟩⟨1|⊗|1⟩⟨0| + U[1, 3]|0⟩⟨1|⊗|1⟩⟨1| + U[2, 0]|1⟩⟨0|⊗|0⟩⟨0| + U[2, 1]|1⟩⟨0|⊗|0⟩⟨1| + U[2, 2]|1⟩⟨1|⊗|0⟩⟨0| + U[2, 3]|1⟩⟨1|⊗|0⟩⟨1| + U[3, 0]|1⟩⟨0|⊗|1⟩⟨0| + U[3, 1]|1⟩⟨0|⊗|1⟩⟨1| + U[3, 2]|1⟩⟨1|⊗|1⟩⟨0| + U[3, 3]|1⟩⟨1|⊗|1⟩⟨1|
- QuantumGate.diagram(
- pad: tuple[int, int] | None = None,
- sep: tuple[int, int] | None = None,
- style: str | None = None,
- return_string: bool | None = None,
Print or return a circuit diagram of the quantum object as a multiline string.
- Parameters:
pad (tuple[int, int]) – A two-tuple describing the horizontal and vertical interior paddings between the content at the centre of the object (e.g., its label) and its outer edge (e.g., block border). Both integers must be non-negative. Defaults to
(0, 0).sep (tuple[int, int]) – A two-tuple describing the horizontal and vertical exterior separation distances at the object’s edges. Both integers must be non-negative. Defaults to
(1, 1).style (str) – A string specifying the style for the circuit visualization to take. Can be any of
"ascii","unicode", or"unicode_alt". Defaults to"unicode".return_string (bool) – Whether to return the assembled diagram as a multiline string. Defaults to
False.
- Returns:
None – Returned only if
return_stringisFalse.str – The rendered circuit diagram. Returned only if
return_stringisTrue.
Note
The quality of the visualization depends greatly on the output’s configuration. For best results, the terminal should have a monospace font with good Unicode coverage.
Examples
For usage examples, please see those of the
QuantumGateclass and its subclasses.
Subclasses#
Please note that the documentation of these subclasses includes only properties and methods that are either new or modified from the base class QuantumGate.
Note
In all of these subclasses, the spec property should not be set.
Subclass |
Alias |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- class Pauli(
- *args,
- index: int,
- **kwargs,
Bases:
QuantumGateA subclass for creating Pauli gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.This is fundamentally a single-system gate, and so a copy is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.index (int) –
The index of the desired Pauli matrix. Can take the following values:
0(\(2\)-dimensional identity matrix \(\Identity\))1(Pauli-X \(\Pauli_x\))2(Pauli-Y \(\Pauli_y\))3(Pauli-Z \(\Pauli_z\))
**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Note
The Pauli gates are defined only for \(2\)-dimensional (i.e., binary/qubit) systems. This means that the constructor does not take
dimas an argument, nor can the associated property be set.Examples
>>> X = Pauli(index=1) >>> X.output() Matrix([ [0, 1], [1, 0]]) >>> X.diagram()
>>> Y = Pauli(index=2) >>> Y.output() Matrix([ [0, -I], [I, 0]]) >>> Y.diagram()
>>> Z = Pauli(index=3) >>> Z.output() Matrix([ [1, 0], [0, -1]]) >>> Z.diagram()
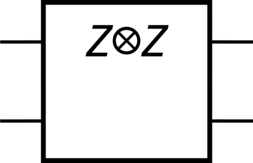
>>> ZZ = Pauli(index=3, targets=[0, 1], label="Z⊗Z") >>> ZZ.output() Matrix([ [1, 0, 0, 0], [0, -1, 0, 0], [0, 0, -1, 0], [0, 0, 0, 1]]) >>> ZZ.diagram()
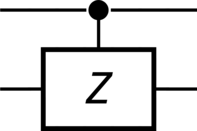
>>> CZ = Pauli(index=3, targets=[1], controls=[0]) >>> CZ.output() Matrix([ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, -1]]) >>> CZ.diagram()
>>> R_xx = Pauli( ... index=1, ... targets=[0, 1], ... exponent="θ/pi", ... coefficient="exp(-I*θ/2)", ... label="R_xx(θ)", ... ) >>> R_xx.output(simplify = True) Matrix([ [ cos(θ/2), 0, 0, -I*sin(θ/2)], [ 0, cos(θ/2), -I*sin(θ/2), 0], [ 0, -I*sin(θ/2), cos(θ/2), 0], [-I*sin(θ/2), 0, 0, cos(θ/2)]]) >>> R_xx.diagram()
- property index: int#
The index of the desired Pauli matrix.
- class GellMann(
- *args,
- index: int,
- **kwargs,
Bases:
QuantumGateA subclass for creating Gell-Mann gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.This is fundamentally a single-system gate, and so a copy is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.index (int) –
The index of the desired Gell-Mann matrix. Can take the following values:
0(\(3\)-dimensional identity matrix \(\Identity\))1(\(\GellMann_1\))2(\(\GellMann_2\))3(\(\GellMann_3\))4(\(\GellMann_4\))5(\(\GellMann_5\))6(\(\GellMann_6\))7(\(\GellMann_7\))8(\(\GellMann_8\))
**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Note
The Gell-Mann gates are defined only for \(3\)-dimensional (i.e., ternary/qutrit) systems. This means that the constructor does not take
dimas an argument, nor can the associated property be set.Examples
>>> L = GellMann(index=8) >>> L.output() Matrix([ [sqrt(3)/3, 0, 0], [ 0, sqrt(3)/3, 0], [ 0, 0, -2*sqrt(3)/3]]) >>> L.diagram()
- property index: int#
The index of the desired Gell-Mann matrix.
- class Rotation(
- *args,
- axis: int,
- angle: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- **kwargs,
Bases:
QuantumGateA subclass for creating rotation gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.The elementary rotation matrices \(\Rotation_i\) are a set of three \(2 \times 2\) matrices,
(294)#\[\begin{split}\begin{aligned} \Rotation_x &= \e^{-\eye\Pauli_{x}\theta/2} = \begin{bmatrix} \cos(\theta/2) & -\eye\sin(\theta/2) \\ -\eye\sin(\theta/2) & \cos(\theta/2) \end{bmatrix} \\ \Rotation_y &= \e^{-\eye\Pauli_{y}\theta/2} = \begin{bmatrix} \cos(\theta/2) & -\sin(\theta/2) \\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix} \\ \Rotation_z &= \e^{-\eye\Pauli_{z}\theta/2} = \begin{bmatrix} \e^{-\eye\theta/2} & 0 \\ 0 & \e^{\eye\theta/2} \end{bmatrix} \end{aligned}\end{split}\]where \(\theta\) is the rotation angle (
angle).These are fundamentally single-system gates, and so a copy of the specified gate is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.axis (int) –
The index corresponding to the axis of the desired rotation matrix. Can take the following values:
1(\(x\)-rotation \(\Rotation_x\))2(\(y\)-rotation \(\Rotation_y\))3(\(z\)-rotation \(\Rotation_z\))
angle (num | sym | str) – The scalar value to be used as the rotation angle. Defaults to
0.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Note
The rotation gates are defined only for \(2\)-dimensional (i.e., binary/qubit) systems. This means that the constructor does not take
dimas an argument, nor can the associated property be set.Examples
>>> R_x = Rotation(axis=1, angle="θ", label="R_x") >>> R_x.output() Matrix([ [ cos(θ/2), -I*sin(θ/2)], [-I*sin(θ/2), cos(θ/2)]]) >>> R_x.diagram()
>>> R_y = Rotation(axis=2, angle="φ", label="R_y") >>> R_y.output() Matrix([ [cos(φ/2), -sin(φ/2)], [sin(φ/2), cos(φ/2)]]) >>> R_y.diagram()
>>> R_z = Rotation(axis=3, angle="t", label="R_z") >>> R_z.output() Matrix([ [exp(-I*t/2), 0], [ 0, exp(I*t/2)]]) >>> R_z.diagram()
- property axis: int#
The index corresponding to the axis of the desired rotation matrix.
- property angle: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str#
The scalar value to be used as the rotation angle.
- class Phase(
- *args,
- phase: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- **kwargs,
Bases:
QuantumGateA subclass for creating phase gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.In \(\Dimension\) dimensions, a phase operator \(\Phase\) may be represented as a \(\Dimension \times \Dimension\) diagonal matrix
(295)#\[\Phase(\omega) = \sum\limits_{k=0}^{\Dimension - 1} \omega^k \ket{k}\bra{k}\]where \(\omega\) is the phase factor.
This is fundamentally a single-system gate, and so a copy is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.phase (num | sym | str) – The phase value. Defaults to the unit root given by
sp.exp(2 * sp.pi * sp.I / self.dim).**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Examples
>>> P = Phase() >>> P.output() Matrix([ [1, 0], [0, -1]]) >>> P.diagram()
>>> S = Phase(exponent=sp.Rational(1, 2), label="S") >>> S.output() Matrix([ [1, 0], [0, I]]) >>> S.diagram()
>>> T = Phase(exponent=sp.Rational(1, 4), label="T") >>> T.output() Matrix([ [1, 0], [0, exp(I*pi/4)]]) >>> D.diagram()
>>> P3 = Phase(dim=3) >>> P3.output() Matrix([ [1, 0, 0], [0, exp(2*I*pi/3), 0], [0, 0, exp(-2*I*pi/3)]]) >>> P3.diagram()
>>> W = Phase(phase="w", dim=3, label="W") >>> W.output() Matrix([ [1, 0, 0], [0, w, 0], [0, 0, w**2]]) >>> W.diagram()
- property phase: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str#
The phase value.
- class Diagonal(
- *args,
- entries: dict[int | list[int], Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str],
- exponentiation: bool | None = None,
- **kwargs,
Bases:
QuantumGateA subclass for creating diagonal gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.In \(\Dimension\) dimensions, a diagonal operator \(\Diagonal\) may be represented as a \(\Dimension \times \Dimension\) diagonal matrix
(296)#\[\Diagonal(\lambda_0, \lambda_1, \ldots, \lambda_{\Dimension - 1}) = \sum\limits_{k=0}^{\Dimension - 1} \lambda_k\ket{k}\bra{k}, \quad \lambda_k \in \Complexes, \; \abs{\lambda_k} = 1\]where \(\{\lambda_k\}_{k=0}^{\Dimension - 1}\) are the main diagonal entries.
This is fundamentally a single-system gate, and so a copy is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.entries (dict[int | list[int], num | sym | str]) – A dictionary in which the keys are level specifications (integer or list of integers) and the values are scalars.
exponentiation (bool) – Whether to exponentiate (with imaginary unit) the values given in
entries. Defaults toFalse.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Note
Levels that are unspecified in the
entriesargument all have a corresponding matrix element of1, regardless of the value ofexponentiation.Examples
>>> D = Diagonal(entries={0: "u", 1: "v"}, exponentiation=False) >>> D.output() Matrix([ [u, 0], [0, v]]) >>> D.diagram()
>>> P = Diagonal( ... entries={1: "p"}, ... exponentiation=True, ... symbols={"p": {"real": True}}, ... label="P", ... ) >>> P.output() Matrix([ [1, 0], [0, exp(I*p)]]) >>> P.diagram()
>>> D3 = Diagonal( ... entries={0: "a", 1: "b", 2: "c"}, ... exponentiation=False, ... symbols={"a": {"real": True}, "b": {"real": True}, "c": {"real": True}}, ... dim=3, ... ) >>> D3.output() Matrix([ [a, 0, 0], [0, b, 0], [0, 0, c]]) >>> D3.diagram()
- property entries: dict[int | list[int], Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str]#
A dictionary in which the keys are level specifications (integer or list of integers) and the values are scalars.
- property exponentiation: bool#
Whether to exponentiate (with imaginary unit) the values given in
entries.
- class Swap(
- *args,
- **kwargs,
Bases:
QuantumGateA subclass for creating SWAP (exchange) gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.In \(\Dimension\) dimensions, a SWAP operator \(\Swap\) between two (neighbouring) systems \(A\) and \(B\) may be represented as a \(\Dimension^2 \times \Dimension^2\) matrix
(297)#\[\Swap^{A,B} = \sum\limits_{j,k=0}^{\Dimension - 1} {\ket{j}\bra{k}}^A \otimes {\ket{k}\bra{j}}^B,\]where the identity operator acts on all other systems.
- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.targets (list[int, int]) – A list of exactly two indices corresponding to the systems to be swapped. Is an argument of the superclass
QuantumGate, so can be specified positionally in*args.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Examples
>>> S = Swap(targets=[0, 1]) >>> S.output() Matrix([ [1, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 0], [0, 0, 0, 1]]) >>> S.diagram()
>>> S3 = Swap(targets=[0, 1], dim=3) >>> S3.output() Matrix([ [1, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 1]]) >>> S3.diagram()
>>> SIS = Swap(targets=[0, 2]) >>> SIS.output() Matrix([ [1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0], [0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1]]) >>> SIS.diagram()
>>> SCS = Swap(targets=[0, 2], controls=[1]) >>> SCS.output() Matrix([ [1, 0, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1]]) >>> SCS.diagram()
>>> RSWAP = Swap(targets=[0, 1], exponent=sp.Rational(1, 2), label="√SWAP", family="GATE") >>> RSWAP.output() Matrix([ [1, 0, 0, 0], [0, 1/2 + I/2, 1/2 - I/2, 0], [0, 1/2 - I/2, 1/2 + I/2, 0], [0, 0, 0, 1]]) >>> RSWAP.diagram()
>>> PSWAP = Swap( ... targets=[0, 1], ... exponent="p", ... symbols={"p": {"real": True}}, ... label="SWAP^p", ... family="GATE", ... ) >>> PSWAP.output() Matrix([ [1, 0, 0, 0], [0, exp(I*pi*p)/2 + 1/2, 1/2 - exp(I*pi*p)/2, 0], [0, 1/2 - exp(I*pi*p)/2, exp(I*pi*p)/2 + 1/2, 0], [0, 0, 0, 1]]) >>> PSWAP.diagram()
>>> CSWAP = Swap(targets=[1, 2], controls=[0]) >>> CSWAP.output() Matrix([ [1, 0, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1]]) >>> CSWAP.diagram()
- class Summation(
- *args,
- shift: int | None = None,
- **kwargs,
Bases:
QuantumGateA subclass for creating SUM (summation) gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.The SUM gate is essentially a generalization of the NOT gate. In \(\Dimension\) dimensions, it is defined as the operator
(298)#\[\SUM(n) = \sum\limits_{k=0}^{\Dimension - 1} \ket{k \oplus n}\bra{k}\]where \(n \in \Integers_{\geq 0}\) (
shift) is the shift parameter, and \(k \oplus n \equiv k + n \mathrel{\mathrm{mod}} \Dimension\).The case of \(n = 1\) is known as the shift operator, and represents a (non-Hermitian) generalization of the Pauli-X \(\Pauli_x\) operator to \(\Dimension\) dimensions.
This is fundamentally a single-system gate, and so a copy is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.shift (int) – The summation shift parameter. Must be a non-negative integer. Defaults to
1.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Examples
>>> SUM = Summation(shift=1) >>> SUM.output() Matrix([ [0, 1], [1, 0]]) >>> SUM.diagram()
>>> SUM3 = Summation(shift=1, dim=3) >>> SUM3.output() Matrix([ [0, 0, 1], [1, 0, 0], [0, 1, 0]]) >>> SUM3.diagram()
- property shift: int#
The summation shift parameter.
- class Not(
- *args,
- **kwargs,
Bases:
SummationA subclass for creating NOT (negation or “bit-flip”) gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.The NOT gate is essentially a specialization of the SUM gate to \(2\)-dimensional (i.e., binary/qubit) systems, and is exactly equivalent to the Pauli-X gate. As such, this class exists purely to simplify access to this operation.
This is fundamentally a single-system gate, and so a copy is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Note
NOT gates are defined only for \(2\)-dimensional (i.e., binary/qubit) systems. This means that the constructor does not take
dimas an argument, nor can the associated property be set.Examples
>>> N = Not(targets=[0]) >>> N.output() Matrix([ [0, 1], [1, 0]]) >>> N.diagram()
>>> NN = Not(targets=[0, 1]) >>> NN.output() Matrix([ [0, 0, 0, 1], [0, 0, 1, 0], [0, 1, 0, 0], [1, 0, 0, 0]]) >>> NN.diagram()
>>> CNOT = Not(targets=[1], controls=[0]) >>> CNOT.output() Matrix([ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0]]) >>> CNOT.diagram()
>>> ANOT = Not(targets=[1], anticontrols=[0]) >>> ANOT.output() Matrix([ [0, 1, 0, 0], [1, 0, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]) >>> ANOT.diagram()
>>> CCNOT = Not(targets=[2], controls=[0, 1]) >>> CCNOT.output() Matrix([ [1, 0, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 1, 0]]) >>> CCNOT.diagram()
>>> RNOT = Not(targets=[0], exponent=sp.Rational(1, 2)) >>> RNOT.output() Matrix([ [1/2 + I/2, 1/2 - I/2], [1/2 - I/2, 1/2 + I/2]]) >>> RNOT.diagram()
- class Hadamard(
- *args,
- **kwargs,
Bases:
QuantumGateA subclass for creating Hadamard gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.The elementary Hadamard gate \(\Hadamard\) (for qubits) may be represented as the \(2 \times 2\) operator
(299)#\[\begin{split}\begin{aligned} \Hadamard &= \frac{1}{\sqrt{2}}\sum\limits_{j,k=0}^{1} (-1)^{jk} \ket{j}\bra{k} \\ &= \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}. \end{aligned}\end{split}\]This can be generalized to the following \(\Dimension\)-dimensional form for qudits,
(300)#\[\begin{split}\begin{aligned} \Hadamard_\Dimension &= \frac{1}{\sqrt{\Dimension}}\sum\limits_{j,k=0}^{\Dimension - 1} \omega_\Dimension^{k(\Dimension - j)} \ket{j}\bra{k} \\ &= \begin{bmatrix} 1 & 1 & 1 & \ldots & 1 \\ 1 & \omega^{\Dimension - 1} & \omega^{2(\Dimension - 1)} & \ldots & \omega^{(\Dimension - 1)^2} \\ 1 & \omega^{\Dimension - 2} & \omega^{2(\Dimension - 2)} & \ldots & \omega^{(\Dimension - 1)(\Dimension - 2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega & \omega^{2} & \ldots & \omega^{\Dimension - 1} \end{bmatrix} \end{aligned}\end{split}\]where \(\omega_\Dimension \equiv \e^{\frac{2\pi\eye}{\Dimension}}\).
This is fundamentally a single-system gate, and so a copy is placed on each of the subsystems corresponding to the indices in the
targetsproperty.- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Examples
>>> H = Hadamard() >>> H.output() Matrix([ [sqrt(2)/2, sqrt(2)/2], [sqrt(2)/2, -sqrt(2)/2]]) >>> H.diagram()
>>> HH = Hadamard(targets=[0, 1], label="H⊗H") >>> HH.output() Matrix([ [1/2, 1/2, 1/2, 1/2], [1/2, -1/2, 1/2, -1/2], [1/2, 1/2, -1/2, -1/2], [1/2, -1/2, -1/2, 1/2]]) >>> HH.diagram()
>>> H3 = Hadamard(dim=3) >>> H3.output() Matrix([ [sqrt(3)/3, sqrt(3)/3, sqrt(3)/3], [sqrt(3)/3, sqrt(3)*exp(-2*I*pi/3)/3, sqrt(3)*exp(2*I*pi/3)/3], [sqrt(3)/3, sqrt(3)*exp(2*I*pi/3)/3, sqrt(3)*exp(-2*I*pi/3)/3]]) >>> H3.diagram()
- class Fourier(
- *args,
- composite: bool | None = None,
- reverse: bool | None = None,
- **kwargs,
Bases:
QuantumGateA subclass for creating Fourier (quantum discrete Fourier transform [QDFT]) gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.The elementary Fourier operator \(\QFT\) for a single \(\Dimension\)-dimensional qudit may be represented as the \(\Dimension \times \Dimension\) matrix
(301)#\[\begin{split}\begin{aligned} \QFT &= \frac{1}{\sqrt{\Dimension}} \sum\limits_{j,k=0}^{\Dimension - 1} \omega_{\Dimension}^{jk} \ket{j}\bra{k} \\ &= \frac{1}{\sqrt{\Dimension}} \begin{bmatrix} 1 & 1 & 1 & 1 & \ldots & 1 \\ 1 & \omega & \omega^2 & \omega^3 & \ldots & \omega^{\Dimension - 1} \\ 1 & \omega^2 & \omega^4 & \omega^6 & \ldots & \omega^{2(\Dimension - 1)} \\ 1 & \omega^3 & \omega^6 & \omega^9 & \ldots & \omega^{3(\Dimension - 1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{\Dimension - 1} & \omega^{2(\Dimension - 1)} & \omega^{3(\Dimension - 1)} & \ldots & \omega^{(\Dimension - 1)(\Dimension - 1)} \\ \end{bmatrix} \end{aligned}\end{split}\]where \(\omega_{\Dimension} = \e^{\frac{2\pi\eye}{\Dimension}} = \omega\).
In the case of \(N\) qudits, the action of the multipartite Fourier operator \(\QFT_N\) on the basis state \(\bigotimes\limits_{\ell=1}^{N} \ket{j_\ell} \equiv \ket{j_1, \ldots, j_N}\) (where \(j_\ell \in \Integers_{0}^{\Dimension - 1}\)) is
(302)#\[\ket{j_1, \ldots, j_N} \stackrel{\QFT_N}{\longrightarrow} \frac{1}{\sqrt{\Dimension^N}} \bigotimes\limits_{\ell=1}^{N} \sum\limits_{k_\ell=0}^{\Dimension - 1} \e^{2\pi\eye j k_\ell \Dimension^{-\ell}} \ket{k_\ell}\]where \(j \equiv \sum\limits_{\ell=1}^{N} j_\ell \Dimension^{N - \ell}\).
If
compositeisTrue, a copy of the elementary form \(\QFT\) is placed on each of the subsystems corresponding to the indices in thetargetsproperty.If
compositeisFalse, the composite form \(\QFT_N\) is applied to the subsystems specified bytargetsin:ascending order if
reverseisFalsedescending order if
reverseisTrue
- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.composite (bool) – Whether the composite (multipartite) Fourier gate is to be used. If
False, copies of the elementary Fourier gate are placed on each index specified intargets. Defaults toTrue.reverse (bool) – Whether to reverse the order in which the composite (multipartite) Fourier gate is applied. Only applies when
compositeisFalse. Defaults toFalse.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Examples
>>> F = Fourier() >>> F.output() Matrix([ [sqrt(2)/2, sqrt(2)/2], [sqrt(2)/2, -sqrt(2)/2]]) >>> F.diagram()
>>> F3 = Fourier(dim=3) >>> F3.output() Matrix([ [sqrt(3)/3, sqrt(3)/3, sqrt(3)/3], [sqrt(3)/3, sqrt(3)*exp(-2*I*pi/3)/3, sqrt(3)*exp(2*I*pi/3)/3], [sqrt(3)/3, sqrt(3)*exp(2*I*pi/3)/3, sqrt(3)*exp(-2*I*pi/3)/3]]) >>> F3.diagram()
>>> FF = Fourier(targets=[0, 1]) >>> FF.output() Matrix([ [1/2, 1/2, 1/2, 1/2], [1/2, -1/2, 1/2, -1/2], [1/2, I/2, -1/2, -I/2], [1/2, -I/2, -1/2, I/2]]) >>> FF.diagram()
- property composite: bool#
Whether the composite (multipartite) Fourier gate is to be used.
- property reverse: bool#
Whether to reverse the order in which the composite (multipartite) Fourier gate is applied. Has no effect when
self.compositeisFalse.
- class Measurement(
- *args,
- operators: list[MutableDenseMatrix | ndarray | QuantumObject],
- observable: bool | None = None,
- **kwargs,
Bases:
QuantumGateA subclass for creating measurement gates and storing their metadata.
This is built upon the
QuantumGateclass, and so inherits all of its attributes, properties, and methods.Instances of this class each describe a (non-linear) operation in which the input state (\(\op{\rho}\)) is quantum-mechanically measured (against the forms in specified in
operators) and subsequently mutated according to its predicted post-measurement form (i.e., the sum of all possible measurement outcomes). This yields the transformed states:When
observableisFalse(operatorsis a list of Kraus operators or projectors \(\Kraus_i\)):
(303)#\[\op{\rho}^\prime = \sum_i \Kraus_i \op{\rho} \Kraus_i^\dagger.\]When
observableisTrue(operatorsis a list of observables \(\Observable_i\)):
(304)#\[\op{\rho}^\prime = \sum_i \trace[\Observable_i \op{\rho}] \Observable_i.\]The items in the list
operatorscan also be vectors (e.g., \(\ket{\xi_i}\)), in which case each is converted into its corresponding matrix representation (e.g., \(\Kraus_i = \ket{\xi_i}\bra{\xi_i}\)) prior to any measurements.Note also that this method does not check for validity of supplied POVMs or the completeness of sets of observables, nor does it renormalize the post-measurement state.
- Parameters:
*args – Variable-length argument list, passed directly to the constructor
__init__of the superclassQuantumGate.operators (list[mat | arr | QuantumObject]) – The operator(s) with which to perform the measurement. These would typically be a (complete) set of Kraus operators forming a POVM, a (complete) set of (orthogonal) projectors forming a PVM, or a set of observables constituting a complete basis for the relevant state space.
observable (bool) – Whether to treat the items in
operatorsas observables (as opposed to Kraus operators or projectors). Defaults toFalse.**kwargs – Arbitrary keyword arguments, passed directly to the constructor
__init__of the superclassQuantumGate.
Note
Measurement operations in quantum physics are, in general, non-linear and non-unitary operations on (normalized) state vectors and density operators. As such, they cannot be represented by matrices, and so the
matrixproperty therefore does not return a valid representation of the measurement operation. Instead, it returns an identity matrix of the appropriate size for its number of dimensions and systems.Note
The
targetsargument must be specified as a list of numerical indices of the subsystem(s) to be measured. These indices must be consecutive, and their number must match the number of systems spanned by all given operators.Examples
>>> from qhronology.mechanics.matrices import ket >>> basis_vectors = [ket(i) for i in [0, 1]] >>> M_basis = Measurement(operators=basis_vectors, observable=False) >>> M_basis.diagram()
>>> pauli_matrices = [Pauli(index=i) for i in [1, 2, 3]] >>> M_pauli = Measurement(operators=pauli_matrices, observable=True, targets=[0], num_systems=2) >>> M_pauli.diagram()
>>> from qhronology.mechanics.matrices import ket >>> plus = (ket(0) + ket(1)) / sp.sqrt(2) >>> minus = (ket(0) - ket(1)) / sp.sqrt(2) >>> M_pm = Measurement(operators=[plus, minus], observable=False, targets=[1], num_systems=2) >>> M_pm.diagram()
- property operators: list[MutableDenseMatrix | ndarray | QuantumObject]#
The operator(s) with which to perform the measurement.
- property observable: bool#
Whether to treat the items in the
operatorsproperty as observables (as opposed to Kraus operators or projectors).
Combining gates#
- class GateInterleave(
- *gates: QuantumGate,
- merge: bool | None = None,
- conjugate: bool | None = None,
- exponent: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- coefficient: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- label: str | None = None,
- notation: str | None = None,
Bases:
QuantumGateCompose two or more
QuantumGateinstances together by interleaving them.This is achieved by multiplying the matrix representations of the gates together. For example, for gates described by the multipartite operators \(\op{A} \otimes \Identity\) and \(\Identity \otimes \op{B}\), their interleaved composition is
(305)#\[(\op{A} \otimes \Identity) \cdot (\Identity \otimes \op{B}) = \op{A} \otimes \op{B}.\]While this is a subclass of
QuantumGate, all of its inherited properties, except for those corresponding to arguments in its constructor, are read-only. This is because they are calculated from their corresponding properties in the individual instances contained within thegatesproperty.- Parameters:
*gates (QuantumGate) – Variable-length argument list of
QuantumGateinstances to be interleaved.merge (bool) – Whether to merge the gates together diagrammatically. Defaults to
False.conjugate (bool) – Whether to perform Hermitian conjugation on the composite gate when it is called. Defaults to
False.exponent (num | sym | str) – A numerical or string representation of a scalar value to which composite gate’s total matrix representation is exponentiated. Must be a non-negative integer. Defaults to
1.coefficient (num | sym | str) – A numerical or string representation of a scalar value by which the composite gate’s matrix representation is multiplied. Performed after exponentiation. Defaults to
1.label (str) – The unformatted string used to represent the gate in mathematical expressions. Defaults to
"⊗".join([gate.label for gate in [*gates]]).notation (str) – The formatted string used to represent the gate in mathematical expressions. When not
None, overrides the value passed tolabel. Not intended to be set by the user in most cases. Defaults toNone.
Note
Care should be taken to ensure that gates passed to this class all have the same
num_systemsvalue and do not have overlappingtargets,controls, andanticontrolsproperties.Note
The resulting visualization (using the inherited
diagram()method or in circuit diagrams) may not be accurate in every case. However, the composed matrix should still be correct.Examples
>>> HI = Hadamard(targets=[0], num_systems=2) >>> IH = Hadamard(targets=[1], num_systems=2) >>> HH = GateInterleave(HI, IH, merge=True) >>> HH.output() Matrix([ [1/2, 1/2, 1/2, 1/2], [1/2, -1/2, 1/2, -1/2], [1/2, 1/2, -1/2, -1/2], [1/2, -1/2, -1/2, 1/2]]) >>> HH.diagram(sep=(1, 2))
>>> XII = Pauli(index=1, targets=[0], num_systems=3) >>> IYI = Pauli(index=2, targets=[1], num_systems=3) >>> IIZ = Pauli(index=3, targets=[2], num_systems=3) >>> XYZ = GateInterleave(XII, IYI, IIZ) >>> XYZ.output() Matrix([ [0, 0, 0, 0, 0, 0, -I, 0], [0, 0, 0, 0, 0, 0, 0, I], [0, 0, 0, 0, I, 0, 0, 0], [0, 0, 0, 0, 0, -I, 0, 0], [0, 0, -I, 0, 0, 0, 0, 0], [0, 0, 0, I, 0, 0, 0, 0], [I, 0, 0, 0, 0, 0, 0, 0], [0, -I, 0, 0, 0, 0, 0, 0]]) >>> XYZ.diagram(sep=(1, 2))
>>> CNII = Not(targets=[1], controls=[0], num_systems=4) >>> IINC = Not(targets=[2], controls=[3], num_systems=4) >>> CNNC = GateInterleave(CNII, IINC) >>> CNNC.diagram()
- property gates: list[QuantumGate]#
Variable-length list of
QuantumGateinstances to be composited.
- property merge: bool#
Whether to merge the gates together diagrammatically.
- class GateStack(
- *gates: QuantumGate,
- merge: bool | None = None,
- conjugate: bool | None = None,
- exponent: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- coefficient: Number | generic | Basic | MatrixSymbol | MatrixElement | Symbol | str | None = None,
- label: str | None = None,
- notation: str | None = None,
Bases:
GateInterleaveCompose two or more
QuantumGateinstances together by “stacking” them vertically.This is achieved by computing the tensor product matrix representations of the gates together. For example, for gates described by the multipartite operators \(\op{A} \otimes \Identity\) and \(\Identity \otimes \op{B}\), their stacked composition is
(306)#\[(\op{A} \otimes \Identity) \otimes (\Identity \otimes \op{B}) = \op{A} \otimes \Identity \otimes \Identity \otimes \op{B}.\]This class is derived from the
QuantumGateclass, and so should be used in much the same way.- Parameters:
*gates (QuantumGate) – Variable-length argument list of
QuantumGateinstances to be stacked.merge (bool) – Whether to merge the gates together diagrammatically. Defaults to
False.conjugate (bool) – Whether to perform Hermitian conjugation on the composite gate when it is called. Defaults to
False.exponent (num | sym | str) – A numerical or string representation of a scalar value to which composite gate’s total matrix representation is exponentiated. Defaults to
1.coefficient (num | sym | str) – A numerical or string representation of a scalar value by which the composite gate’s matrix representation is multiplied. Performed after exponentiation. Defaults to
1.label (str) – The unformatted string used to represent the gate in mathematical expressions. Defaults to
"⊗".join([gate.label for gate in [*gates]]).notation (str) – The formatted string used to represent the gate in mathematical expressions. When not
None, overrides the value passed tolabel. Not intended to be set by the user in most cases. Defaults toNone.
Examples
>>> X = Pauli(index=1) >>> Y = Pauli(index=2) >>> Z = Pauli(index=3) >>> XYZ = GateStack(X, Y, Z) >>> XYZ.output() Matrix([ [0, 0, 0, 0, 0, 0, -I, 0], [0, 0, 0, 0, 0, 0, 0, I], [0, 0, 0, 0, I, 0, 0, 0], [0, 0, 0, 0, 0, -I, 0, 0], [0, 0, -I, 0, 0, 0, 0, 0], [0, 0, 0, I, 0, 0, 0, 0], [I, 0, 0, 0, 0, 0, 0, 0], [0, -I, 0, 0, 0, 0, 0, 0]]) >>> XYZ.diagram(sep=(1, 2))
>>> gates = [Not(targets=[(i + 1) % 2], controls=[i % 2]) for i in range(0, 4)] >>> CNOTs = GateStack(*gates) >>> CNOTS.diagram()
>>> gates = [GellMann(index=i) for i in range(1, 9)] >>> L = GateStack(*gates) >>> L.diagram(sep=(1, 1))