Closed timelike curves and time machines#
Closed timelike curves (CTCs) form an interesting class of objects within the general theory of relativity as they present the possibility for an observer to travel back in time. Formally, a CTC is an entirely geometric entity, being simply a curve (a path in spacetime) that is both closed and everywhere (either future- or past-directed) timelike. As such, in a universe with CTCs, any physical system may be able to interact with its past self, and so the potential existence of CTCs within our own universe naturally evokes scientific investigation into time travel. The foremost focus of such research is on questions regarding the non-trivial causal structure of CTC spacetimes and the consistency of the standard laws of physics.
In some locally unobjectionable exact solutions to the Einstein field equations, CTCs naturally occur [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]. However, many such spacetimes are often considered to be globally unphysical (like the classic swirling dust solutions of van Stockum [3] and Gödel [5]), and so the presence of interior CTCs is usually considered to be an artefact of the theory. Despite this, it is believed that CTCs may be constructed (at least theoretically) through the use of a traversable wormhole [2, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 42, 43, 44, 45, 46, 47, 48]. It is important to stress however that the physicality of such models is often called into question in the literature. This is due mainly to the fact that these solutions to the Einstein field equations often appear to necessitate the existence of matter possessing a negative energy density, and as such they do not always correspond to stable spacetimes. Note therefore that other solutions (such as the Kerr metric [8]), being free of the requirement of negative energy density, may enable the manifestation of CTCs in a much less contentious manner.
Wormhole-based time machines#
In popular culture, wormholes (either artificially constructed or naturally occurring) commonly provide a means of interstellar (or even intergalactic) transportation. They accomplish this by allowing spaceships to quickly traverse their short, tubiform interiors and emerge at distant locations far sooner than any alternative non-wormhole routes would allow. Alternatively, if two separate moments in time were to be linked by wormhole instead of two separate locations, one would possess a time machine [2, 26, 49, 50, 1], i.e., a mechanism which can produce CTCs. Thus, wormholes are theoretically able to facilitate both long-distance space travel and time travel. It is this basis on which many of the studies involving wormhole-based time machines is established.
In essence, a wormhole is an exotic, theoretical object that connects two distant regions in space. The simplest version of a topological wormhole [2, 2, 3, 3] can be constructed by “cutting out” two spatially separated balls (denoted by \(\Mouth^\pm\), representing the two ends of the wormhole) in flat three-dimensional space and subsequently “gluing” (connecting) the surfaces (denoted by \(\partial\Mouth^\pm\)) of these holes together. The resulting mouths (entrances) into the wormhole are thus identified, which is to say that entering into one results in simultaneous emergence from the other. See Figure 2 for a visual depiction of such geometry. Note that the resulting spacetime is topologically and geometrically non-trivial since the space is not simply connected and the identified surfaces are not flat.
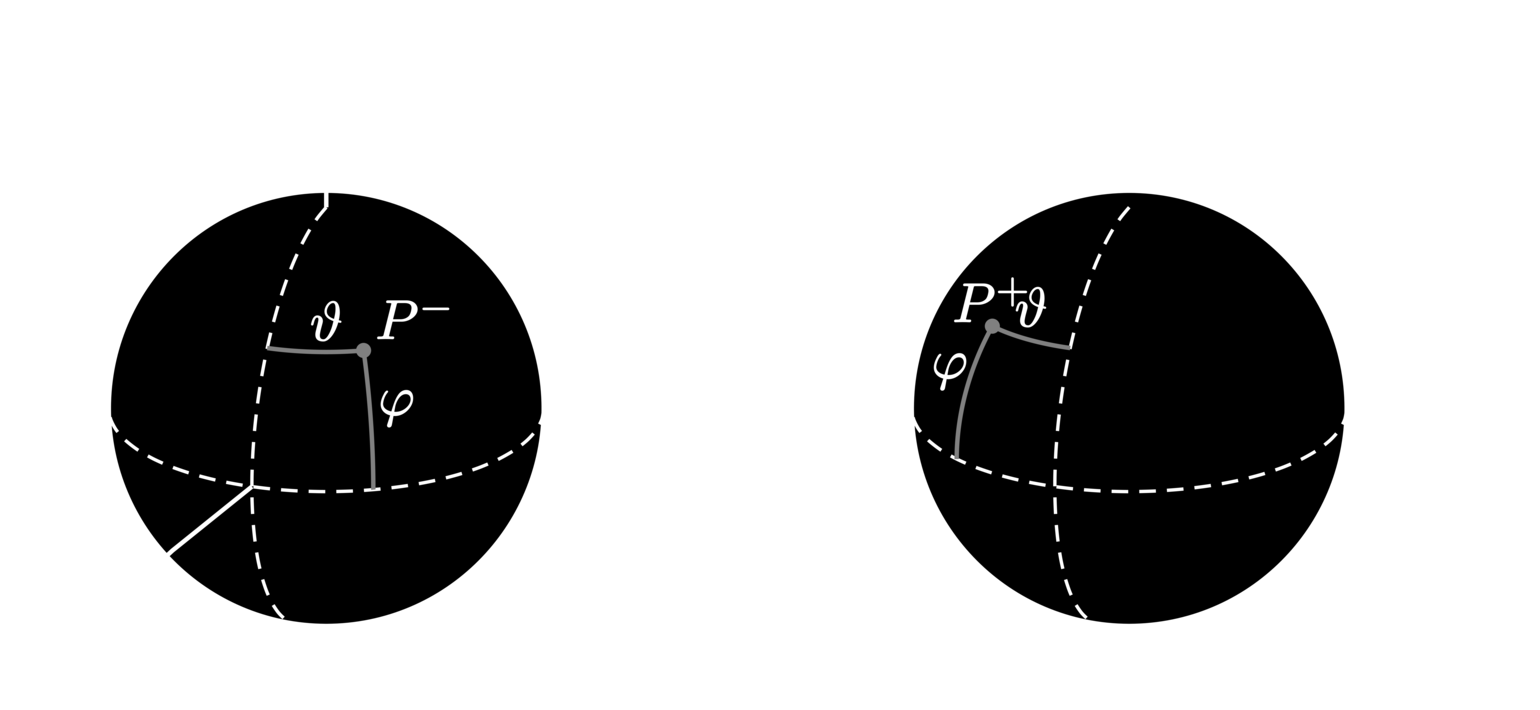
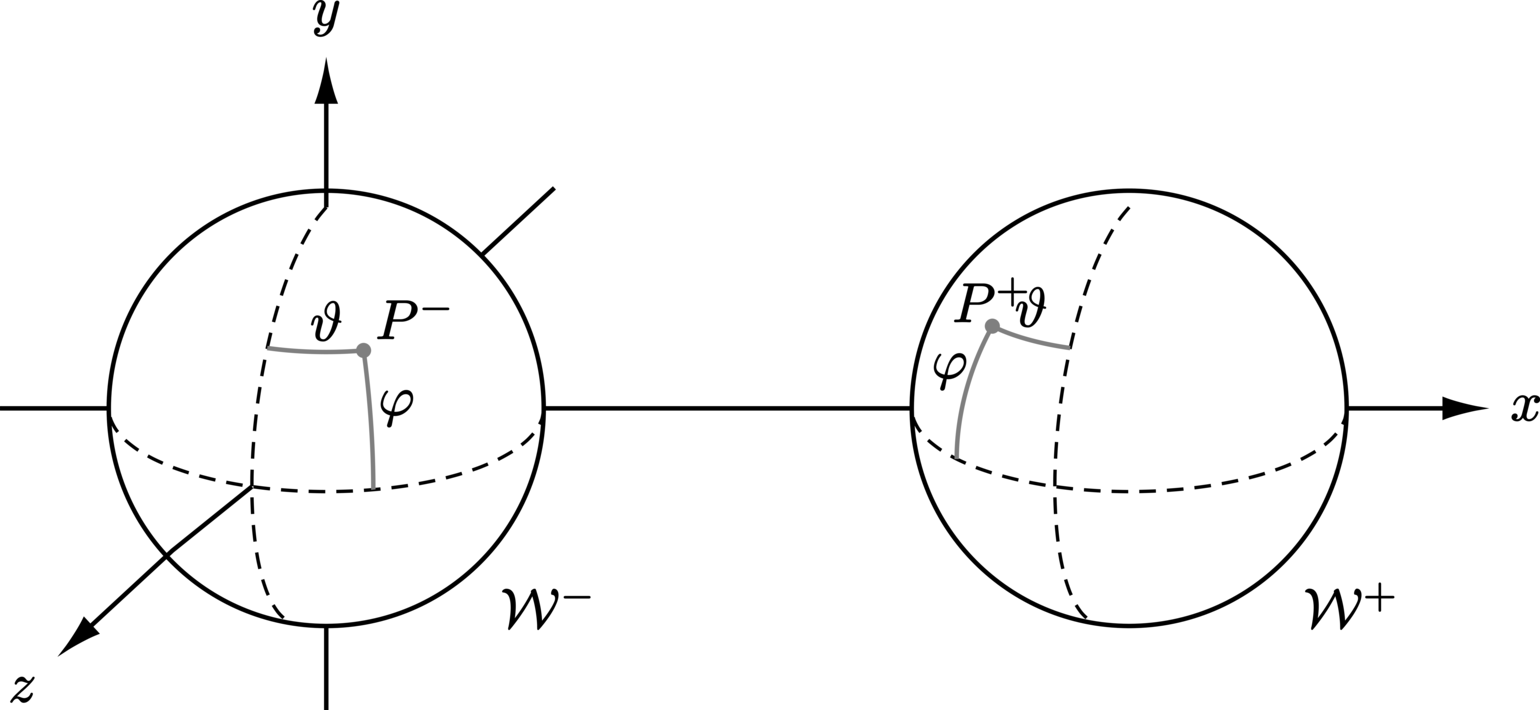
To turn a wormhole into a time machine (thereby manifesting CTCs), a time “delay” has to be induced between the mouths. This can be accomplished in a few different ways, resulting in either of two distinct classes of time machine. The first class consists of those of which the time machine is eternal (meaning that CTCs are ever-present), and is accomplished simply by imposing a identification time difference (denoted \(\TimeDelta\)) between the two mouths (so that the coordinate time \(\Time\) on the “future” mouth \(\MouthFuture\) corresponds to the time \((\Time - \TimeDelta)\) on the “past” mouth \(\MouthPast\)). The second class consists of those created (theoretically) in a more physically realistic manner, such as moving one mouth (the future mouth) either into a strong gravitational field or accelerating it to relativistic speeds (and decelerating it back) [2]. For both classes of wormhole-based time machines, when the temporal difference between the mouths reaches a greater magnitude than their spatial separation, the mouths become causally connected, that is, CTCs manifest.
Time-travel paradoxes#
The emergence of inconsistencies due to retro-causal action in the evolution of a time-travelling physical system is an issue which is captured by the infamous grandfather paradox (detailed in [31]). This problem, which is perhaps the foremost example of a time-travel paradox, takes on many forms, all of which share the common characteristic of antichronological causation. The archetype of the paradox often features an observer who travels to the past and, through their actions (usually by interfering with the relationship between their young grandparents), prevents their own birth. Consequently, the observer is unable to travel back in time to preclude their existence, thus the paradox is evident.
The principle of self-consistency#
Time-travel paradoxes and the concept of retro-causality lie at the foundation of the issues with CTCs. In particular, the inconsistencies associated with paradoxical causal sequences have led to uncertainty regarding the pathology of CTCs and hence their research suitability. However, there is a distinct lack of evidence suggesting that the inconsistencies of CTC paradoxes are entirely inescapable. One may simply regard these problems as ill-posed, given that the initial conditions (e.g., the observer’s very existence and intent to intervene) are influenced by the future occurrences (e.g., observer stopping their grandparents from ever meeting). To resolve this problem, we could suppose that there exists some fundamental characteristic of reality which forbids any future event from paradoxically altering the past.
In particular, we could conjecture the existence of an innate law by which the universe operates, called the principle of self-consistency [2], which prohibits paradoxical causal sequences from transpiring. Under this condition, a globally consistent solution of the local physical laws must exist. This means that, while a system is allowed to propagate into its own past, it must do so in a way that is consistent with its own original history. Any interaction that occurs must be compatible with the past, and causal sequences containing events solely of this nature are characterized as being self-consistent.
References
K. Lanczos, “Über eine stationäre Kosmologie im Sinne der Einsteinschen Gravitationstheorie”, Zeitschrift für Physik, 21(1):73–110, December 1924. https://doi.org/10.1007/BF01328251, doi:10.1007/BF01328251
T. Lewis, “Some special solutions of the equations of axially symmetric gravitational fields”, Proc. R. Soc. Lond. A, 136(829):176–192, May 1932. http://rspa.royalsocietypublishing.org/content/136/829/176, doi:10.1098/rspa.1932.0073
W. J. van Stockum, “The Gravitational Field of a Distribution of Particles Rotating about an Axis of Symmetry”, Proceedings of the Royal Society of Edinburgh, 57:135–154, 1938. https://www.cambridge.org/core/journals/proceedings-of-the-royal-society-of-edinburgh/article/ixthe-gravitational-field-of-a-distribution-of-particles-rotating-about-an-axis-of-symmetry/40E39372658C7031B0C4316A36154F46, doi:10.1017/S0370164600013699
A. Papapetrou, “A Static Solution of the Equations of the Gravitational Field for an Arbitary Charge-Distribution”, Proceedings of the Royal Irish Academy. Section A: Mathematical and Physical Sciences, 51:191–204, 1945. http://www.jstor.org/stable/20488481
K. Gödel, “An Example of a New Type of Cosmological Solutions of Einstein's Field Equations of Gravitation”, Reviews of Modern Physics, 21(3):447–450, July 1949. https://link.aps.org/doi/10.1103/RevModPhys.21.447, doi:10.1103/RevModPhys.21.447
A. H. Taub, “Empty Space-Times Admitting a Three Parameter Group of Motions”, Annals of Mathematics, 53(3):472–490, 1951. http://www.jstor.org/stable/1969567, doi:10.2307/1969567
E. T. Newman, L. A. Tamburino, and T. W. J. Unti, “Empty‐Space Generalization of the Schwarzschild Metric”, Journal of Mathematical Physics, 4(7):915–923, July 1963. http://aip.scitation.org/doi/10.1063/1.1704018, doi:10.1063/1.1704018
R. P. Kerr, “Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics”, Physical Review Letters, 11(5):237–238, September 1963. https://link.aps.org/doi/10.1103/PhysRevLett.11.237, doi:10.1103/PhysRevLett.11.237
H. Levy and W. J. Robinson, “The rotating body problem”, Mathematical Proceedings of the Cambridge Philosophical Society, 60(2):279–285, April 1964. https://www.cambridge.org/core/journals/mathematical-proceedings-of-the-cambridge-philosophical-society/article/rotating-body-problem/BFCD29EC2C11E38FD0E2200B658D5456, doi:10.1017/S0305004100037750
A. Papapetrou, “Champs gravitationnels stationnaires à symétrie axiale”, Ann.Inst.H.Poincare Phys.Theor., 4:83–105, 1966. http://www.numdam.org/item/AIHPA_1966__4_2_83_0/
F. J. Tipler, “Rotating cylinders and the possibility of global causality violation”, Physical Review D, 9(8):2203–2206, April 1974. https://link.aps.org/doi/10.1103/PhysRevD.9.2203, doi:10.1103/PhysRevD.9.2203
I.Damião Soares, “Inhomogeneous rotating universes with closed timelike geodesics of matter”, Journal of Mathematical Physics, 21(3):521–525, March 1980. https://aip.scitation.org/doi/10.1063/1.524437, doi:10.1063/1.524437
J. R. Gott, “Closed timelike curves produced by pairs of moving cosmic strings: Exact solutions”, Physical Review Letters, 66(9):1126–1129, March 1991. https://link.aps.org/doi/10.1103/PhysRevLett.66.1126, doi:10.1103/PhysRevLett.66.1126
W. B. Bonnor, “An exact, asymptotically flat, vacuum solution of Einstein's equations with closed timelike curves”, Classical and Quantum Gravity, 19(23):5951–5957, November 2002. https://doi.org/10.1088/0264-9381/19/23/305, doi:10.1088/0264-9381/19/23/305
W. B. Bonnor and B. R. Steadman, “The double-Kerr solution”, Classical and Quantum Gravity, 21(11):2723–2732, May 2004. https://doi.org/10.1088/0264-9381/21/11/014, doi:10.1088/0264-9381/21/11/014
A. Ori, “A Class of Time-Machine Solutions with a Compact Vacuum Core”, Physical Review Letters, 95(2):021101, July 2005. https://link.aps.org/doi/10.1103/PhysRevLett.95.021101, doi:10.1103/PhysRevLett.95.021101
W. B. Bonnor and B. R. Steadman, “Exact solutions of the Einstein-Maxwell equations with closed timelike curves”, General Relativity and Gravitation, 37(11):1833–1844, November 2005. https://doi.org/10.1007/s10714-005-0163-3, doi:10.1007/s10714-005-0163-3
A. Ori, “Formation of closed timelike curves in a composite vacuum/dust asymptotically flat spacetime”, Physical Review D, 76(4):044002, August 2007. https://link.aps.org/doi/10.1103/PhysRevD.76.044002, doi:10.1103/PhysRevD.76.044002
D. Sarma, M. Patgiri, and F. U. Ahmed, “Pure radiation metric with stable closed timelike curves”, General Relativity and Gravitation, 46(1):1633, December 2013. https://doi.org/10.1007/s10714-013-1633-7, doi:10.1007/s10714-013-1633-7
B. K. Tippett and D. Tsang, “Traversable acausal retrograde domains in spacetime”, Classical and Quantum Gravity, 34(9):095006, March 2017. https://doi.org/10.1088/1361-6382/aa6549, doi:10.1088/1361-6382/aa6549
D. Fermi and L. Pizzocchero, “A time machine for free fall into the past”, Classical and Quantum Gravity, 35(16):165003, July 2018. https://doi.org/10.1088/1361-6382/aace6e, doi:10.1088/1361-6382/aace6e
T. C. Ralph and C. Chang, “Spinning up a time machine”, Physical Review D, 102(12):124013, December 2020. https://link.aps.org/doi/10.1103/PhysRevD.102.124013, doi:10.1103/PhysRevD.102.124013
H. G. Ellis, “Ether flow through a drainhole: A particle model in general relativity”, Journal of Mathematical Physics, 14(1):104–118, January 1973. http://aip.scitation.org/doi/abs/10.1063/1.1666161, doi:10.1063/1.1666161
S. W. Hawking, “Wormholes in spacetime”, Physical Review D, 37(4):904–910, February 1988. https://link.aps.org/doi/10.1103/PhysRevD.37.904, doi:10.1103/PhysRevD.37.904
M. S. Morris and K. S. Thorne, “Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity”, American Journal of Physics, 56(5):395–412, May 1988. https://aapt.scitation.org/doi/10.1119/1.15620, doi:10.1119/1.15620
M. S. Morris, K. S. Thorne, and U. Yurtsever, “Wormholes, Time Machines, and the Weak Energy Condition”, Physical Review Letters, 61(13):1446–1449, September 1988. https://link.aps.org/doi/10.1103/PhysRevLett.61.1446, doi:10.1103/PhysRevLett.61.1446
M. Visser, “Traversable wormholes: Some simple examples”, Physical Review D, 39(10):3182–3184, May 1989. https://link.aps.org/doi/10.1103/PhysRevD.39.3182, doi:10.1103/PhysRevD.39.3182
M. Visser, “Traversable wormholes from surgically modified Schwarzschild spacetimes”, Nuclear Physics B, 328(1):203–212, December 1989. https://www.sciencedirect.com/science/article/pii/0550321389901004, doi:10.1016/0550-3213(89)90100-4
D. H. Coule and K. I. Maeda, “Wormholes with scalar fields”, Classical and Quantum Gravity, 7(6):955–963, June 1990. https://doi.org/10.1088%2F0264-9381%2F7%2F6%2F005, doi:10.1088/0264-9381/7/6/005
M. Visser, “Van Vleck determinants: Traversable wormhole spacetimes”, Physical Review D, 49(8):3963–3980, April 1994. https://link.aps.org/doi/10.1103/PhysRevD.49.3963, doi:10.1103/PhysRevD.49.3963
M. Visser, Lorentzian Wormholes: From Einstein to Hawking, AIP Press, American Institute of Physics, 1995.
M. Visser, “Traversable wormholes: The Roman ring”, Physical Review D, 55(8):5212–5214, April 1997. https://link.aps.org/doi/10.1103/PhysRevD.55.5212, doi:10.1103/PhysRevD.55.5212
A. Carlini, D. H. Coule, and D. M. Solomons, “Euclidean Quantum Wormholes with Scalar Fields”, International Journal of Modern Physics A, 12(20):3517–3544, August 1997. http://www.worldscientific.com/doi/abs/10.1142/S0217751X97001821, doi:10.1142/S0217751X97001821
D. Hochberg and M. Visser, “Geometric structure of the generic static traversable wormhole throat”, Physical Review D, 56(8):4745–4755, October 1997. https://link.aps.org/doi/10.1103/PhysRevD.56.4745, doi:10.1103/PhysRevD.56.4745
C. Barceló and M. Visser, “Traversable wormholes from massless conformally coupled scalar fields”, Physics Letters B, 466(2):127–134, November 1999. https://www.sciencedirect.com/science/article/pii/S037026939901117X, doi:10.1016/S0370-2693(99)01117-X
C. Barceló and M. Visser, “Scalar fields, energy conditions and traversable wormholes”, Classical and Quantum Gravity, 17(18):3843–3864, September 2000. https://doi.org/10.1088/0264-9381/17/18/318, doi:10.1088/0264-9381/17/18/318
C. Barceló and M. Visser, “Brane surgery: energy conditions, traversable wormholes, and voids”, Nuclear Physics B, 584(1):415–435, September 2000. https://www.sciencedirect.com/science/article/pii/S0550321300003795, doi:10.1016/S0550-3213(00)00379-5
N. Dadhich, S. Kar, S. Mukherjee, and M. Visser, “\$R=0\$ spacetimes and self-dual Lorentzian wormholes”, Physical Review D, 65(6):064004, February 2002. https://link.aps.org/doi/10.1103/PhysRevD.65.064004, doi:10.1103/PhysRevD.65.064004
M. Visser, S. Kar, and N. Dadhich, “Traversable Wormholes with Arbitrarily Small Energy Condition Violations”, Physical Review Letters, 90(20):201102, May 2003. https://link.aps.org/doi/10.1103/PhysRevLett.90.201102, doi:10.1103/PhysRevLett.90.201102
S. Kar, N. Dadhich, and M. Visser, “Quantifying energy condition violations in traversable wormholes”, Pramana, 63(4):859–864, October 2004. https://doi.org/10.1007/BF02705207, doi:10.1007/BF02705207
T. C. Ralph and T. G. Downes, “Relativistic quantum information and time machines”, Contemporary Physics, 53(1):1–16, January 2012. http://www.tandfonline.com/doi/abs/10.1080/00107514.2011.640146, doi:10.1080/00107514.2011.640146
N. M. Garcia, F. S. N. Lobo, and M. Visser, “Generic spherically symmetric dynamic thin-shell traversable wormholes in standard general relativity”, Physical Review D, 86(4):044026, August 2012. https://link.aps.org/doi/10.1103/PhysRevD.86.044026, doi:10.1103/PhysRevD.86.044026
L. M. Butcher, “Traversable wormholes and classical scalar fields”, Physical Review D, 91(12):124031, June 2015. https://link.aps.org/doi/10.1103/PhysRevD.91.124031, doi:10.1103/PhysRevD.91.124031
K. A. Bronnikov, “Scalar fields as sources for wormholes and regular black holes”, Particles, 1(1):56–81, December 2018. https://www.mdpi.com/2571-712X/1/1/5, doi:10.3390/particles1010005
A. Simpson, P. Martín-Moruno, and M. Visser, “Vaidya spacetimes, black-bounces, and traversable wormholes”, Classical and Quantum Gravity, 36(14):145007, June 2019. https://doi.org/10.1088/1361-6382/ab28a5, doi:10.1088/1361-6382/ab28a5
P. Cañate, J. Sultana, and D. Kazanas, “Ellis wormhole without a phantom scalar field”, Physical Review D, 100(6):064007, September 2019. https://link.aps.org/doi/10.1103/PhysRevD.100.064007, doi:10.1103/PhysRevD.100.064007
F. S. N. Lobo, A. Simpson, and M. Visser, “Dynamic thin-shell black-bounce traversable wormholes”, Physical Review D, 101(12):124035, June 2020. https://link.aps.org/doi/10.1103/PhysRevD.101.124035, doi:10.1103/PhysRevD.101.124035
T. Berry, F. S. N. Lobo, A. Simpson, and M. Visser, “Thin-shell traversable wormhole crafted from a regular black hole with asymptotically Minkowski core”, Physical Review D, 102(6):064054, September 2020. https://link.aps.org/doi/10.1103/PhysRevD.102.064054, doi:10.1103/PhysRevD.102.064054
I. D. Novikov, “Analysis of the operation of a time machine”, Zhurnal Éksperimental'noĭ i Teoreticheskoĭ Fiziki, 95(3):769–776, March 1989. http://jetp.ras.ru/cgi-bin/e/index/r/95/3/p769?a=list
K. S. Thorne, “Do the laws of physics permit closed timelike curves?”, Annals of the New York Academy of Sciences, 631(1):182–193, August 1991. http://nyaspubs.onlinelibrary.wiley.com/doi/abs/10.1111/j.1749-6632.1991.tb52642.x, doi:10.1111/j.1749-6632.1991.tb52642.x
A. S. Lossev and I. D. Novikov, “The jinn of the time machine: nontrivial self-consistent solutions”, Classical and Quantum Gravity, 9(10):2309, 1992. https://iopscience.iop.org/article/10.1088/0264-9381/9/10/014, doi:10.1088/0264-9381/9/10/014
J. Friedman, M. S. Morris, I. D. Novikov, F. Echeverria, G. Klinkhammer, K. S. Thorne, and U. Yurtsever, “Cauchy problem in spacetimes with closed timelike curves”, Physical Review D, 42(6):1915–1930, September 1990. https://link.aps.org/doi/10.1103/PhysRevD.42.1915, doi:10.1103/PhysRevD.42.1915
J. L. Friedman and M. S. Morris, “The Cauchy problem for the scalar wave equation is well defined on a class of spacetimes with closed timelike curves”, Physical Review Letters, 66(4):401–404, January 1991. https://link.aps.org/doi/10.1103/PhysRevLett.66.401, doi:10.1103/PhysRevLett.66.401
J. L. Friedman and M. S. Morris, “Existence and Uniqueness Theorems for Massless Fields on a Class of Spacetimes with Closed Timelike Curves”, Communications in Mathematical Physics, 186(3):495–529, July 1997. https://doi.org/10.1007/s002200050118, doi:10.1007/s002200050118
J. L. Friedman, “The Cauchy Problem on Spacetimes That Are Not Globally Hyperbolic”, The Einstein Equations and the Large Scale Behavior of Gravitational Fields, pages 331–346, Birkhäuser, Basel, 2004. https://link.springer.com/chapter/10.1007/978-3-0348-7953-8_9, doi:10.1007/978-3-0348-7953-8_9