The Deutsch model (D-CTCs)

In 1991, David Deutsch introduced a method of analysing the flow of information in a chronology-violating network. This prescription, now known as the Deutsch model [3], consists of a quantum theory of computation applied to a CTC model where most of the geometry has been abstracted away. It is based on the requirement that time evolution of the local density operator (taken as a fundamental object) of a quantum system must be self-consistent.

One of the main results of Deutsch’s work on time travel is his proposal for the time evolution of quantum states through a quantum circuit representation of a chronology-violating network (illustrated in Figure 4), with particular note as to how it resolves time-travel paradoxes and indeterminism.

Figure 4 Deutsch’s model of quantum time travel.

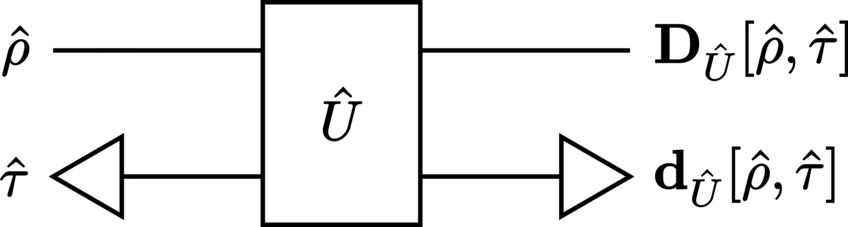
The mathematical formulation of his self-consistent evolution of a quantum state through a region with a time machine is provided by requiring that any given chronology-violating (CV) system enters the CTC in the state

(220)\[\StateCV \in \SpaceMixed(\SpaceHilbert_\CV),\]

and then emerges in the past in the same state despite having interacted with a chronology-respecting (CR) system in the state

(221)\[\StateCR \in \SpaceMixed(\SpaceHilbert_\CR)\]

through a unitary \(\Unitary\) on \(\SpaceHilbert_\CR\otimes\SpaceHilbert_\CV\). The joint density operator entering the gate is simply the tensor product \(\StateCR \otimes \StateCV\) on \(\SpaceHilbert_\CR\otimes\SpaceHilbert_\CV\) so that the standard evolution through the unitary is given by

(222)\[\StateCR \otimes \StateCV \rightarrow \MapGeneral_{\Unitary}[\StateCR \otimes \StateCV] = \Unitary(\StateCR \otimes \StateCV)\Unitary^\dagger.\]

We can now trace the CV and CR subsystems out and denote the resulting maps as

(223)\[\begin{aligned} \MapDCTCsCV_{\Unitary}[\StateCR,\StateCV] &\equiv \trace_\CR\bigl[\Unitary(\StateCR \otimes \StateCV)\Unitary^\dagger\bigr], \end{aligned}\]

(224)\[\begin{aligned} \MapDCTCsCR_{\Unitary}[\StateCR,\StateCV] &\equiv \trace_\CV\bigl[\Unitary(\StateCR \otimes \StateCV)\Unitary^\dagger\bigr]. \end{aligned}\]

Self-consistent solutions of the CTC state may then be identified as fixed points of the CV map (223), which are expressible via

(225)\[\StateCV = \MapDCTCsCV_{\Unitary}[\StateCR,\StateCV].\]

This condition essentially codifies the requirement that the “younger” CTC state (the right-hand side) exiting the gate is the same as the “older” CTC state (the left-hand side) entering the gate. Once solutions to equation (225) are determined, the evolution of the system state \(\StateCR\) through the interaction \(\Unitary\) in this Deutsch model is then simply given by the CR map (224). Deutsch’s original construction specifically interprets D-CTCs as being portals between parallel universes—a time traveller on a D-CTC would pass in and out of such universes—and so the quantum states in this context describes a superposition of states where the time traveller does and does not exist.

The fact that the imposed self-consistency constraint in (225) is a fixed-point condition means that the non-linearity introduced to the laws of quantum mechanics is distinct from that of other models. Furthermore, as the rigid matching requirement is for the density matrix as opposed to the individual states in a pure state decomposition, the Deutsch model intrinsically treats density matrices ontologically as ontic (“real”) objects rather than as epistemic knowledge representations.

Deutsch’s picture: The rule of maximum entropy

Of crucial significance is the fact that the Deutsch prescription resolves time-travel paradoxes without placing any constraints on the input system state. This is because Deutsch proved that at least one consistent solution of the (normalized) map

(226)\[\begin{aligned} \normalized{\MapDCTCsCV_{\Unitary}^{\infty}}[\StateCR,\StateCV^{(0)}] \equiv \lim_{N\rightarrow\infty}\frac{1}{N+1} \sum_{k=0}^{N}\MapDCTCsCV_{\Unitary}^{k}(\StateCR,\StateCV^{(0)}) \end{aligned}\]

exists for every unitary \(\Unitary\) and input \(\StateCR\). Here, \(\StateCV^{(0)} \in \SpaceLinear(\SpaceHilbert_\CV)\) represents some initial CV state, and \(\MapDCTCsCV^{k}\) denotes \(k\) compositions of the D-CTC CV map, i.e.,

(227)\[\begin{split}\begin{aligned} \MapDCTCsCV^{k}_{\Unitary}\bigl[\StateCR,\StateCV^{(0)}\bigr] &= (\,\underbrace{\MapDCTCsCV_{\Unitary} \circ \MapDCTCsCV_{\Unitary} \circ \ldots \circ \MapDCTCsCV_{\Unitary}}_{k \text{ times}}\,)\bigl[\StateCR,\StateCV^{(0)}\bigr] \\ &= \MapDCTCsCV_{\Unitary}\biggl[ \StateCR,\MapDCTCsCV_{\Unitary}\Bigl[ \StateCR,\ldots,\MapDCTCsCV_{\Unitary}\bigl[\StateCR,\StateCV^{(0)}\bigr] \Bigr] \biggr]. \end{aligned}\end{split}\]

Note however that some interactions have a multiplicity of fixed points, which leads to non-determinism in the time evolution. This characteristic, known as the uniqueness ambiguity in the context of D-CTCs, may be interpreted as an indication that the theory is incomplete.

To overcome this problem, Deutsch argued that the “correct” solution is the one with the most von Neumann entropy (157). This proposition appeals to the principles of thermodynamics (the second law in particular), and asserts that the trapped CTC would naturally tend towards a maximally entropic equilibrium state. Given its lack of rigorous theoretical support however, Deutsch’s rule of maximum entropy is often considered to be an unsatisfactory approach to overcoming the problem of plurality in the CTC state solution.

Iterative picture: The equivalent circuit

In 2010, Ralph and Myers introduced their equivalent-circuit picture (ECP) [2, 4, 5, 6, 7] of the D-CTC model. This approach was formulated as a method of deriving the maximum entropy rule and thus resolving the uniqueness ambiguity. It consists of essentially “unwrapping” the D-CTC time-loop fixed-point circuit (Figure 4) into an infinite sequence of interactions with perfect copies of the input state, and is illustrated in Figure 5.

Figure 5 The equivalent-circuit picture of a D-CTC.

In this model, the CTC-trapped state \(\StateCV^{(n-1)}\) enters the \(n\)th interaction \(\Unitary\) and exits, according to the fixed-point condition (225), in the state

(228)\[\StateCV^{(n)} = \MapDCTCsCV_{\Unitary}[\StateCR,\StateCV^{(n-1)}].\]

The final output \(\StateCV^{(\infty)}\) is then obtained by applying this map recursively ad infinitum to an initial state \(\StateCV^{(0)}\). Accordingly, one finds, in the limit,

(229)\[\StateCV^{(\infty)} = \lim_{N \rightarrow\infty}\MapDCTCsCV_{\Unitary}^{N}[\StateCR,\StateCV^{(0)}]\]

Given this framework, the ECP then introduces an arbitrarily small decoherence interaction \(\Decoherence\), parametrized by the decoherence strength \(0<\delta\ll1\), to each CTC iteration,

(230)\[\begin{split}\begin{aligned} \StateCV^{(n)} &= \Decoherence\bigl[\MapDCTCsCV_{\Unitary}[\StateCR,\StateCV^{(n-1)}]\bigr] \\ &= (1-\delta)\MapDCTCsCV_{\Unitary}[\StateCR,\StateCV^{(n-1)}] + \delta\normalized{\Identity} \end{aligned}\end{split}\]

where

(231)\[\begin{split}\begin{aligned} \normalized{\Identity} &\equiv \frac{1}{\dim(\SpaceHilbert)}\Identity, \\ \Identity &\equiv \sum_{i}^{\dim(\SpaceHilbert)}\ket{i}\bra{i} \in \SpaceHilbert, \end{aligned}\end{split}\]

are the unnormalized and normalized maximally mixed (identity) states, respectively. The corresponding final output is then

(232)\[\StateCV^{(\infty)} = \lim_{N\rightarrow\infty}\left[(1-\delta)^{N}\MapDCTCsCV_{\Unitary}^{N}[\StateCR,\StateCV^{(0)}] + \sum_{k=0}^{N-1}\delta^{k}(1-\delta)^{k}\MapDCTCsCV_{\Unitary}^{k}[\StateCR,\normalized{\Identity}]\right].\]

From this result, it can be determined that the non-uniqueness in the solutions to the CV CTC map corresponds to sensitivity to the initial condition \(\StateCV^{(0)}\). Ralph and Myers then show that the result of (232) converges to the unique solution of Deutsch’s maximum entropy rule, and that this rule and result coincides with setting the initial state to be the maximally mixed CTC state \(\StateCV^{(0)}=\normalized{\Identity}\) in (229). The appealing feature of this picture is that Deutsch’s maximum entropy rule is not merely a postulate of the theory; rather, it is a direct result.

Later, Allen [1] noticed that the equivalent circuit does not always converge when there is decoherence interaction, and that Ralph and Myers’s proof of the derivation of the maximum entropy rule was incomplete. However, Dong [7] then showed that the ECP leads instead to a revised maximum entropy rule, one which is distinct from (and perhaps more valid than) Deutsch’s original rule. It asserts that, when multiple valid solutions of the CV map exist, the Deutsch model “chooses” the stable fixed-point state with the most entropy (as determined by the equivalent model with a decoherence interaction). Additionally, note that the final fixed point as given by this revised rule is in general dependent on the decoherence strength (\(\delta\)).

Allen’s picture: Noise incorporation

In 2014, Allen [1] proposed a different method of resolving the uniqueness ambiguity. It consists of the incorporation of noise into the CV channel via a noise channel \(\Depolarization\) with depolarization parameter \(0<\nu<1\), which is accomplished by

(233)\[\begin{split}\begin{aligned} \StateCV &= \Depolarization\bigl[\MapDCTCsCV_{\Unitary}[\StateCR,\StateCV]\bigr] \\ &= (1-\nu)\MapDCTCsCV_{\Unitary}[\StateCR,\StateCV] + \nu\normalized{\Identity}. \end{aligned}\end{split}\]

Allen then proves that this addition resolves the uniqueness ambiguity without requiring a maximum entropy rule, and that the unique fixed-point CTC state is \(\StateCV^{(0)}\)-independent and given by

(234)\[\begin{aligned} \normalized{\Depolarization[\MapDCTCsCV_{\Unitary}^{\infty}]}(\StateCR) = \lim_{N\rightarrow\infty}\frac{1}{N+1} \sum_{k=0}^{N}\Depolarization\bigl[\MapDCTCsCV_{\Unitary}^{k}[\StateCR,\StateCV^{(0)}]\bigr]. \end{aligned}\]

Given that \(\Depolarization\) is a noise channel, then it should be strictly contractive (that is, its trace distance should always decrease under its action), leaving (234) unique. Dong [7] then show that Allen’s picture is inequivalent to both Deutsch’s and Ralph and Myers’s pictures.

References

[1] (1,2)

J.-M. A. Allen, “Treating time travel quantum mechanically”, Physical Review A, 90(4):042107, October 2014. https://link.aps.org/doi/10.1103/PhysRevA.90.042107, doi:10.1103/PhysRevA.90.042107

[2]

T. C. Ralph and T. G. Downes, “Relativistic quantum information and time machines”, Contemporary Physics, 53(1):1–16, January 2012. http://www.tandfonline.com/doi/abs/10.1080/00107514.2011.640146, doi:10.1080/00107514.2011.640146

[3]

D. Deutsch, “Quantum mechanics near closed timelike lines”, Physical Review D, 44(10):3197–3217, November 1991. https://link.aps.org/doi/10.1103/PhysRevD.44.3197, doi:10.1103/PhysRevD.44.3197

[4]

T. C. Ralph and C. R. Myers, “Information flow of quantum states interacting with closed timelike curves”, Physical Review A, 82(6):062330, December 2010. https://link.aps.org/doi/10.1103/PhysRevA.82.062330, doi:10.1103/PhysRevA.82.062330

[5]

T. C. Ralph and C. R. Myers, “Reply to “Comment on ‘Information flow of quantum states interacting with closed timelike curves’””, Physical Review A, 84(5):056302, November 2011. https://link.aps.org/doi/10.1103/PhysRevA.84.056302, doi:10.1103/PhysRevA.84.056302

[6]

J. L. Pienaar, C. R. Myers, and T. C. Ralph, “Quantum fields on closed timelike curves”, Physical Review A, 84(6):062316, December 2011. https://link.aps.org/doi/10.1103/PhysRevA.84.062316, doi:10.1103/PhysRevA.84.062316

[7] (1,2,3)

X. Dong, H. Chen, and L. Zhou, “Ralph's equivalent circuit model, revised Deutsch's maximum entropy rule and discontinuous quantum evolutions in D-CTCs”, arXiv:1711.06814 [quant-ph], November 2017. http://arxiv.org/abs/1711.06814