Postselected teleportation (P-CTCs)

The other main prescription of the quantum mechanics of time travel, postselected teleportation (P-CTCs) [4, 5] (based on unpublished work in [6], and also due independently to [7] as discussed in [8]), also provides self-consistent resolutions to general time-travel paradoxes. P-CTCs are motivated as mechanisms for facilitating the quantum teleportation of quantum systems to the past [6]. The contemporary mathematical description of the prescription is based upon postselection, and essentially consists of a quantum communication channel that is formed through teleportation.

The CV (CTC) quantum channel is replaced with a maximally entangled state \(\ket{\Bell}\) (i.e., a Bell state for qubits), allowing for states to be transported between a sender and receiver through shared entanglement. Quantum teleportation further combined with postselection results in a quantum channel to the past. Antichronological time travel then manifests due to the entanglement between the forward and backward parts of the curve, and one thus obtains a possible theoretical description of quantum mechanics near CTCs. Note that the replacement of the CTC channel with the postselection of a maximally entangled state is equivalent to a path-integral formulation (developed in [3]) in which the CTC state’s wave function evolves in accordance with self-consistent boundary conditions (specifically, the initial and final coordinates are the same). This is why we say that P-CTCs has the important feature of being equivalent to the path-integral formulation of quantum mechanics. Here, we demonstrate the model.

The path-integral formulation in the presence of CTCs

The path-integral formulation of quantum mechanics allows us to formulate the transition amplitude for a quantum system which evolves from an initial state \(\ket{\WaveFunctionInitial}\) to a final state \(\ket{\WaveFunctionFinal}\) as an integral over the paths of the action. In one spatial dimension \(\Position(\Time)\), we may simply write

(235)\[\bra{\WaveFunctionFinal}\Unitary(\TimeFinal,\TimeInitial)\ket{\WaveFunctionInitial} = \iint\diff{\PositionInitial}\,\diff{\PositionFinal} \, \WaveFunctionInitial(\PositionInitial) \conj{\WaveFunctionFinal}{(\PositionFinal)}\int_{\PositionInitial}^{\PositionFinal} \DifferentialPath^{\prime}\Position \, \e^{\eye \Action[\Position]/\hbar}.\]

Here, \(\Unitary(\TimeFinal,\TimeInitial)\) is the time-evolution operator that describes the state evolution from initial time \(\TimeInitial\) to final time \(\TimeFinal\),

(236)\[\begin{split}\begin{aligned} \Position(\TimeInitial) &\equiv \PositionInitial, \\ \Position(\TimeFinal) &\equiv \PositionFinal, \end{aligned}\end{split}\]

are the initial and final coordinates respectively,

(237)\[\begin{split}\begin{aligned} \ket{\WaveFunctionInitial} &= \int \diff{\PositionInitial} \, \WaveFunctionInitial(\PositionInitial)\ket{\PositionInitial}, \\ \ket{\WaveFunctionFinal} &= \int \diff{\PositionFinal} \, \WaveFunctionFinal(\PositionFinal)\ket{\PositionFinal}, \end{aligned}\end{split}\]

are the position representations of the initial and final states, and

(238)\[\Action[\Position] \equiv \int_{\TimeInitial}^{\TimeFinal} \Lagrangian\bigl(\Time,\Position(\Time),\dot{\Position}(\Time)\bigr) \, \diff{\Time},\]

is the action of path \(\Position(\Time)\) with Lagrangian \(\Lagrangian\bigl(\Time,\Position(\Time),\dot{\Position}(\Time)\bigr)\).

To incorporate a CTC into the path-integral formulation, we first divide the spacetime into two parts, or more formally, two separate systems: a CR system \(\ket{\WaveFunction}\in\SpaceHilbert_\CR\) and a CV system \(\ket{\WaveFunctionCTC}\in\SpaceHilbert_\CV\). Let their position-space representations be parametrized by the coordinates \(u\) and \(v\) respectively, so that the initial and final position representations are

(239)\[\begin{split}\begin{aligned} \ket{\WaveFunctionInitial} &= \int \diff{u^{\prime}} \, \WaveFunctionInitial(u^{\prime})\ket{u^{\prime}} \quad &\rightarrow \quad \ket{\WaveFunctionFinal} &= \int \diff{u^{\prime\prime}} \, \WaveFunctionInitial(u^{\prime\prime})\ket{u^{\prime\prime}}, \\ \ket{\WaveFunctionCTCInitial} &= \int \diff{v^{\prime}} \, \WaveFunctionCTCInitial(v^{\prime})\ket{v^{\prime}} \quad &\rightarrow \quad \ket{\WaveFunctionCTCFinal} &= \int \diff{v^{\prime\prime}} \,\WaveFunctionCTCInitial(v^{\prime\prime})\ket{v^{\prime\prime}}. \end{aligned}\end{split}\]

This means that, with time-evolution unitary \(\Unitary(\TimeInitial,\TimeFinal)\) on \(\SpaceHilbert_\CR\otimes\SpaceHilbert_\CV\), the joint input state evolves as per \(\ket{\WaveFunctionInitial}\otimes\ket{\WaveFunctionCTCInitial} \rightarrow \ket{\WaveFunctionFinal}\otimes\ket{\WaveFunctionCTCFinal}\) over the spatial coordinates \((u^{\prime},v^{\prime})\rightarrow(u^{\prime\prime},v^{\prime\prime})\). Using equation (235), this evolution has a corresponding path-integral representation of

(240)\[\begin{aligned} \bigl(\bra{\WaveFunctionFinal}\otimes\bra{\WaveFunctionCTCFinal}\bigr)\Unitary(\TimeFinal,\TimeInitial)\bigl(\ket{\WaveFunctionInitial}\otimes\ket{\WaveFunctionCTCInitial}\bigr) &= \iiiint\diff{u^{\prime}}\,\diff{u^{\prime\prime}}\,\diff{v^{\prime}}\,\diff{v^{\prime\prime}} \, \WaveFunctionInitial(u^{\prime}) \conj{\WaveFunctionFinal}{(u^{\prime\prime})}\WaveFunctionCTCInitial(v^{\prime}) \conj{\WaveFunctionCTCFinal}{(v^{\prime\prime})} \int_{(u^{\prime},v^{\prime})}^{(u^{\prime\prime},v^{\prime\prime})} \DifferentialPath^{\prime}\Position \, \e^{\eye \Action[\Position]/\hbar}. \end{aligned}\]

Now, to include a CTC in this scheme, we mandate that the initial and final coordinates for the chronology-violating system are the same, just like in a CTC. Mathematically, we impose the boundary condition \(v^{\prime}=v^{\prime\prime}\) a \(\delta\)-function in (240), and the resulting transition amplitude for the chronology-respecting system with an incorporated CTC may be written as

(241)\[\bigl(\bra{\WaveFunctionFinal}\otimes\Identity\bigr)\Unitary(\TimeFinal,\TimeInitial)\bigl(\ket{\WaveFunctionInitial}\otimes\Identity\bigr) = \iiiint\diff{u^{\prime}}\,\diff{u^{\prime\prime}}\,\diff{v^{\prime}}\,\diff{v^{\prime\prime}} \, \WaveFunctionInitial(u^{\prime}) \conj{\WaveFunctionFinal}{(u^{\prime\prime})} \delta(v^{\prime}-v^{\prime\prime}) \int_{(u^{\prime},v^{\prime})}^{(u^{\prime\prime},v^{\prime\prime})} \DifferentialPath^{\prime}\Position \, \e^{\eye \Action[\Position]/\hbar}.\]

The coherent addition of all possible initial and final conditions for the CTC is captured through the \(v^{\prime}\) and \(v^{\prime\prime}\) integrals, hence the removal of the CTC states \(\ket{\WaveFunctionCTCInitial}\) and \(\ket{\WaveFunctionCTCFinal}\). This indicates that it is not possible to assign a state to the CTC system (at least in this context), which in turn means that compatibility with the boundary conditions implies that the CR system is not in a forbidden state.

Equivalence of CTC path integrals and postselected teleportation

Given the form (241) of the transition amplitude obtained using path-integral methods, we now wish to show that it is equal to the form which one obtains from postselected teleportation methods. To do this, let us first define our maximally entangled bipartite state of choice \(\ket{\Bell}\in\SpaceHilbert_\CV\otimes\SpaceHilbert_\Teleportation\) in a \(w\)-space representation as

(242)\[\ket{\Bell} = \int \diff{w} \, \Bell(w) \, \ket{w}\otimes\ket{w}\]

where we assume that \(\Bell(w)\) satisfies the normalization condition

(243)\[1 = \braket{\Bell}{\Bell} = \int \diff{w}\, \abs{\Bell(w)}^2.\]

Furthermore, note how (242) can be put in a more useful form by using a \(\delta\)-function,

(244)\[\ket{\Bell} = \iint \diff{v}\,\diff{w} \, \Bell(v,w)\delta(v-w) \ket{v}\otimes\ket{w}.\]

From here, we replace the CV state \(\ket{\WaveFunctionCTC}\) with the maximally entangled \(\ket{\Bell}\), thereby meaning that our input state \(\ket{\WaveFunctionInitial}\otimes\ket{\WaveFunctionCTCInitial}\) evolves under a transformation described by the composition \(\Unitary(\TimeFinal,\TimeInitial)\otimes\Identity\). To clarify, the time-evolution operator \(\Unitary\) only acts on the \(\SpaceHilbert_\CR\) (CR) and \(\SpaceHilbert_\CV\) (CV) Hilbert spaces while the identity \(\Identity\) acts on the third (teleportation) Hilbert space \(\SpaceHilbert_\Teleportation\). With this, we then postselect on the output being in the state \(\ket{\WaveFunctionFinal}\otimes\ket{\Bell}\), which physically represents the teleportation Hilbert space \(\SpaceHilbert_\Teleportation\) being used to send this conditional selection back in time, thereby yielding the necessary postselected teleportation. This entire sequence can be formulated by replacing the CTC state in (240) with our maximally entangled state (244), which yields

(245)\[\begin{split}\begin{aligned} \bigl(\bra{\WaveFunctionFinal}\otimes\bra{\Bell}\bigr)\bigl(\Unitary(\TimeFinal,\TimeInitial)\otimes\Identity\bigr)\bigl(\ket{\WaveFunctionInitial}\otimes\ket{\Bell}\bigr) &= \iint \diff{v^{\prime\prime}}\,\diff{w^{\prime\prime}}\,\conj{\Bell}{(v^{\prime\prime},w^{\prime\prime})}\delta(v^{\prime\prime}-w^{\prime\prime})\bigl(\bra{\WaveFunctionFinal}\otimes\bra{v^{\prime\prime}}\otimes\bra{w^{\prime\prime}}\bigr) \\ &\quad\times\bigl(\Unitary(\TimeFinal,\TimeInitial)\otimes\Identity\bigr)\\ &\quad\times\iint \diff{v^{\prime}}\,\diff{w^{\prime}}\,\Bell(v^{\prime},w^{\prime})\delta(v^{\prime}-w^{\prime})\bigl(\ket{\WaveFunctionInitial}\otimes\ket{v^{\prime}}\otimes\ket{w^{\prime}}\bigr)\\ &= \iiiint \diff{v^{\prime}}\,\diff{v^{\prime\prime}}\,\diff{w^{\prime}}\,\diff{w^{\prime\prime}}\,\Bell(v^{\prime},w^{\prime})\conj{\Bell}{(v^{\prime\prime},w^{\prime\prime})}\delta(v^{\prime}-w^{\prime})\delta(v^{\prime\prime}-w^{\prime\prime}) \\ &\quad\times\bigl(\bra{\WaveFunctionFinal}\otimes\bra{v^{\prime\prime}}\otimes\bra{w^{\prime\prime}}\bigr)\bigl(\Unitary^{\prime}(\TimeFinal,\TimeInitial)\otimes\Identity\bigr)\bigl(\ket{\WaveFunctionInitial}\otimes\ket{v^{\prime}}\otimes\ket{w^{\prime}}\bigr)\\ &= \iiiint \diff{v^{\prime}}\,\diff{v^{\prime\prime}}\,\diff{w^{\prime}}\,\diff{w^{\prime\prime}}\,\Bell(v^{\prime},w^{\prime})\conj{\Bell}{(v^{\prime\prime},w^{\prime\prime})}\delta(v^{\prime}-w^{\prime})\delta(v^{\prime\prime}-w^{\prime\prime}) \\ &\quad\times\iint \diff{u^{\prime}}\,\diff{u^{\prime\prime}}\, \WaveFunctionInitial(u^{\prime})\conj{\WaveFunctionFinal}{(u^{\prime\prime})}\int_{(u^{\prime},v^{\prime})}^{(u^{\prime\prime},v^{\prime\prime})} \DifferentialPath^{\prime}\Position \, \e^{\eye \Action[\Position]/\hbar} \cdot \underbrace{\bra{w^{\prime\prime}}\Identity\ket{w^{\prime}}}_{=\delta(w^{\prime\prime}-w^{\prime})} \\ &= \iiint \diff{v^{\prime}}\,\diff{v^{\prime\prime}}\,\diff{w^{\prime}}\,\Bell(v^{\prime},w^{\prime})\conj{\Bell}{(v^{\prime\prime},w^{\prime})}\delta(v^{\prime}-w^{\prime})\delta(v^{\prime\prime}-w^{\prime}) \\ &\quad\times\iint \diff{u^{\prime}}\,\diff{u^{\prime\prime}}\, \WaveFunctionInitial(u^{\prime})\conj{\WaveFunctionFinal}{(u^{\prime\prime})}\int_{(u^{\prime},v^{\prime})}^{(u^{\prime\prime},v^{\prime\prime})} \DifferentialPath^{\prime}\Position \, \e^{\eye \Action[\Position]/\hbar} \\ &= \iint \diff{v^{\prime}}\,\diff{v^{\prime\prime}}\,\Bell(v^{\prime})\conj{\Bell}{(v^{\prime\prime})}\delta(v^{\prime}-v^{\prime\prime}) \\ &\quad\times\iint \diff{u^{\prime}}\,\diff{u^{\prime\prime}}\, \WaveFunctionInitial(u^{\prime})\conj{\WaveFunctionFinal}{(u^{\prime\prime})}\int_{(u^{\prime},v^{\prime})}^{(u^{\prime\prime},v^{\prime\prime})} \DifferentialPath^{\prime}\Position \, \e^{\eye \Action[\Position]/\hbar} \\ &= \iiiint \diff{u^{\prime}}\,\diff{u^{\prime\prime}}\,\diff{v^{\prime}}\,\diff{v^{\prime\prime}}\,\WaveFunctionInitial(u^{\prime})\conj{\WaveFunctionFinal}{(u^{\prime\prime})}\delta(v^{\prime}-v^{\prime\prime}) \\ &\quad\times\int_{(u^{\prime},v^{\prime})}^{(u^{\prime\prime},v^{\prime\prime})} \DifferentialPath^{\prime}\Position \, \e^{\eye \Action[\Position]/\hbar}. \end{aligned}\end{split}\]

Thus, we can see that the path-integral formulation (241) is equivalent to postselection (245), that is,

(246)\[\bigl(\bra{\WaveFunctionFinal}\otimes\Identity\bigr)\Unitary(\TimeFinal,\TimeInitial)\bigl(\ket{\WaveFunctionInitial}\otimes\Identity\bigr) = \bigl(\bra{\WaveFunctionFinal}\otimes\bra{\Bell}\bigr)\bigl(\Unitary(\TimeFinal,\TimeInitial)\otimes\Identity\bigr)\bigl(\ket{\WaveFunctionInitial}\otimes\ket{\Bell}\bigr).\]

Of course, being based on the path-integral formulation, these quantities are in general not normalized, and so must be renormalized in order to ensure that the probabilistic interpretation of the theory remains intact.

General form of P-CTC system evolution

Here we show how a CR system state \(\StateCR\in\SpaceHilbert_\CR\) in the Dirac bra-ket formalism evolves through the postselected teleportation chronology-violating network depicted in Figure 6.

Figure 6 The postselected teleportation model of quantum time travel.

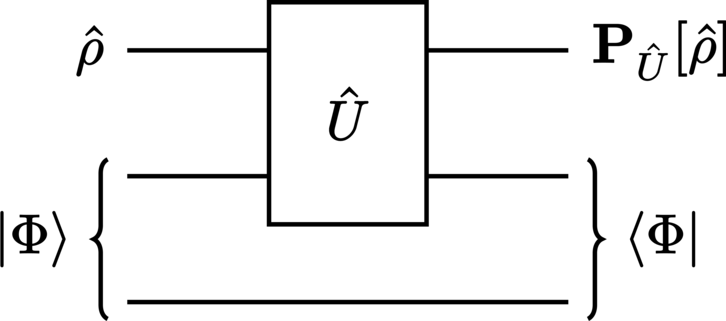
In the P-CTCs formalism, self-consistent resolutions to quantum time-travel paradoxes are provided by way of quantum teleportation. This is achieved by first introducing a teleportation system to the pre-existing CR and CV pair. On the CV and teleportation modes, a maximally entangled state \(\ket{\Bell} \in \SpacePure(\SpaceHilbert_\CV \otimes \SpaceHilbert_\Teleportation)\) is placed (preselected). Here, \(\SpaceHilbert_\Teleportation\) is the Hilbert space of the teleportation system. With this, the evolution of the product input state \(\StateCR \otimes \ket{\Bell}\bra{\Bell}\) under the unitary \(\Unitary \otimes \Identity\) is simply

(247)\[\StateCR \otimes \ket{\Bell}\bra{\Bell} \rightarrow \MapGeneral_{\Unitary \otimes \Identity}[\StateCR \otimes \ket{\Bell}\bra{\Bell}] = \bigl(\Unitary \otimes \Identity\bigr)\bigl(\StateCR \otimes \ket{\Bell}\bra{\Bell}\bigr)\bigl(\Unitary^\dagger \otimes \Identity\bigr).\]

In accordance with the protocol of quantum teleportation, subsequent postselection against the same entangled state results in a quantum channel to the past (on the system \(\SpaceHilbert_\Teleportation\)). Mathematically, the evolved CR state becomes

(248)\[\begin{split}\begin{aligned} \MapPCTCsCR_{\Unitary}[\StateCR] &\propto \bigl(\Identity \otimes \bra{\Bell}\bigr)\bigl(\Unitary \otimes \Identity\bigr)\bigl(\StateCR \otimes \ket{\Bell}\bra{\Bell}\bigr)\bigl(\Unitary^\dagger \otimes \Identity\bigr)\bigl(\Identity \otimes \ket{\Bell}\bigr) \\ &= \trace_\CV[\Unitary]\,\StateCR\,\trace_\CV[\Unitary^\dagger], \end{aligned}\end{split}\]

where we computed

(249)\[\bigl(\Identity \otimes \bra{\Bell}\bigr)\bigl(\Unitary \otimes \Identity\bigr)\bigl(\Identity \otimes \ket{\Bell}\bigr) \propto \trace_\CV[\Unitary].\]

The P-CTCs evolution of the input state \(\StateCR\) is then given by the renormalized form of the non-unitary map (248), that is,

(250)\[\MapPCTCsCR_{\Unitary}[\StateCR] = \frac{\OperatorPCTC \StateCR \OperatorPCTC^\dagger}{\trace[ \OperatorPCTC \StateCR \OperatorPCTC^\dagger]}.\]

where we defined the P-CTC operator

(251)\[\OperatorPCTC \equiv \trace_\CV[\Unitary].\]

In the case of a pure CR input state \(\StateCR = \ket{\StatePure}\bra{\StatePure}\), the associated P-CTC CR map on the corresponding vector state is simply

(252)\[\MapPCTCsCR_{\Unitary}\bigl[\ket{\StatePure}\bigr] = \frac{\OperatorPCTC \ket{\StatePure}}{\sqrt{ \bigl| \bigl| \OperatorPCTC \ket{\StatePure} \bigr| \bigr|}}.\]

As each \(\StateCR\) is mapped onto a specific \(\MapPCTCsCR_{\Unitary}[\StateCR]\) by (250), P-CTCs do not suffer from uniqueness ambiguities, unlike D-CTCs. An important point to note however is that because (251) is not in general unitary, the theory must be renormalized, which preserves its probabilistic interpretation at the cost of linearity.

Determination of the P-CTC CV state

A striking observation in a comparison of D-CTCs and P-CTCs is the sheer incompatibility between them. Of their many differences, perhaps the most perplexing of all is that one cannot assign a state to the system on the P-CTC [5], while the determinability of the state on the D-CTC is crucial to the success of the theory. For the former, provided all boundary conditions in the path-integral picture [3] are satisfied by the CV state (residing on the P-CTC), then the ability of the P-CTC prescription to resolve any given time-travel paradox is entirely independent of, and agnostic to, this state. The D-CTC model on the other hand relies fundamentally on the CV state being definable, as it is upon this object which the notion of temporal self-consistency is imposed, with the CR output state being directly dependent on it.

Although the state on the P-CTC is ordinarily unassignable, the P-CTC itself is the conduit by which information is necessarily transported to the past. In principle, this means that some CV state exists physically, and so must admit a definite form. It is therefore natural to ponder exactly what state the quantum system on the P-CTC assumes for any given scenario. A methodology which provides the ability to investigate the CV states in quantum prescriptions of time travel would therefore be both useful and enlightening.

To solve this problem, one might think of employing the well-established technique of quantum state tomography [1, 2, 9, 10, 11]. This essentially consists of the determination of an unknown quantum state by measuring it with respect to all elements of an appropriate tomographically or informationally complete basis (set of observables). Examples of such bases include the Pauli matrices (plus the identity matrix) (130) for qubits, and the Gell-Mann matrices (also with the identity) (136) for qutrits. Once the unknown state (or rather, an ensemble of identically prepared quantum states) has been measured exhaustively in a suitable basis, the resulting statistics (i.e., expectation values) enable the determination of the Bloch vector via (139), which is equivalent to precise identification of the associated (and previously unknown) state.

At first glance, this could conceivably allow for the determination of the state of the time-travelling (CV) system in any given quantum prescription of antichronological time travel. A problem with this methodology however is its incompatibility with the requirement of resolving the state without simultaneously disturbing it (i.e., collapsing the wave function). Such a feature is essential, as an ordinary (“strong”) measurement would necessarily disturb the CV state, thereby disrupting the relevant self-consistency condition(s) in any given quantum formulation of CTCs (like D-CTCs and P-CTCs). Therefore, in order to measure the state on the CTC without (significantly) perturbing the system, one can use so-called weak measurements [19, 20, 23, 29, 12, 13, 14, 15, 16, 17, 18, 21, 22, 24, 25, 26, 27, 28], that is, quantum measurements which minimize disturbance by leaving the measured state unaffected (to first order). This technique and its findings were first presented in [30].

Using this methodology, it is possible to rigorously assign a state to the system on the P-CTC, with such a state taking the form

(253)\[\MapPCTCsCV_{\Unitary}[\StateCR] \equiv \trace_\CR\bigl[\Unitary(\StateCR \otimes \tfrac{1}{2}\Identity)\Unitary^\dagger\bigr].\]

In contrast to its D-CTC counterpart, this state can be computed (and is in fact also unique) for every given combination of interaction \(\Unitary\) and input state \(\StateCR\). Another interesting observation is that it is exactly equivalent to the CV output state from the first iteration of a maximally mixed seed state in the D-CTC ECP (see Iterative picture: The equivalent circuit). In essence, this means that a P-CTC can be thought of as being somewhat like a “partial” D-CTC—one in which the self-consistency condition is not fully realized (at least according to D-CTCs). This is curious result, as it suggests that despite their striking differences, the distinct notions of self-consistency that underpin both P-CTCs and D-CTCs may be more similar than traditionally thought.

An important point to note is that the result (253) is applicable only to \(2\)-dimensional (qubit) systems, and that a similar expression for \(\Dimension\)-dimensional (qudit) systems has yet to be determined analytically. One such candidate however is the natural generalization

(254)\[\MapPCTCsCV_{\Unitary}[\StateCR] \equiv \trace_\CR\bigl[\Unitary(\StateCR \otimes \tfrac{1}{\Dimension}\Identity)\Unitary^\dagger\bigr].\]

It is important to reiterate that while this expression may seem perfectly reasonable, its validity as the P-CTC CV state has not been proven. While likely highly non-trivial, it is expected however that such generalization is an entirely possible task. Therefore, an interesting next step would be to study the application of the weak-measurement tomography scheme to \(\Dimension\)-level (qudit) systems, as such work should provide more insight into the generality of the methodology and its results.

References

[1]

M. Nielsen and I. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press, Cambridge, 2010.

[2]

R. T. Thew, K. Nemoto, A. G. White, and W. J. Munro, “Qudit quantum-state tomography”, Physical Review A, 66(1):012303, July 2002. https://link.aps.org/doi/10.1103/PhysRevA.66.012303, doi:10.1103/PhysRevA.66.012303

[3] (1,2)

H. D. Politzer, “Path integrals, density matrices, and information flow with closed timelike curves”, Physical Review D, 49(8):3981–3989, April 1994. https://link.aps.org/doi/10.1103/PhysRevD.49.3981, doi:10.1103/PhysRevD.49.3981

[4]

S. Lloyd, L. Maccone, R. Garcia-Patron, V. Giovannetti, Y. Shikano, S. Pirandola, L. A. Rozema, A. Darabi, Y. Soudagar, L. K. Shalm, and A. M. Steinberg, “Closed Timelike Curves via Postselection: Theory and Experimental Test of Consistency”, Physical Review Letters, 106(4):040403, January 2011. https://link.aps.org/doi/10.1103/PhysRevLett.106.040403, doi:10.1103/PhysRevLett.106.040403

[5] (1,2)

S. Lloyd, L. Maccone, R. Garcia-Patron, V. Giovannetti, and Y. Shikano, “Quantum mechanics of time travel through post-selected teleportation”, Physical Review D, 84(2):025007, July 2011. https://link.aps.org/doi/10.1103/PhysRevD.84.025007, doi:10.1103/PhysRevD.84.025007

[6] (1,2)

C. H. Bennett and B. Schumacher, “Simulated time travel, teleportation without communication, and how to conduct a romance with someone who has fallen into a black hole”, May 2005. http://www.research.ibm.com/people/b/bennetc/QUPONBshort.pdf

[7]

G. Svetlichny, “Effective Quantum Time Travel”, 50(12):3903–3914, February 2009. http://arxiv.org/abs/0902.4898

[8]

G. Svetlichny, “Time Travel: Deutsch vs. Teleportation”, International Journal of Theoretical Physics, 50(12):3903–3914, December 2011. https://doi.org/10.1007/s10773-011-0973-x, doi:10.1007/s10773-011-0973-x

[9]

D. F. V. James, P. G. Kwiat, W. J. Munro, and A. G. White, “Measurement of qubits”, Physical Review A, 64(5):052312, October 2001. https://link.aps.org/doi/10.1103/PhysRevA.64.052312, doi:10.1103/PhysRevA.64.052312

[10]

G. Mauro D’Ariano, M. G. A. Paris, and M. F. Sacchi, “Quantum Tomography”, P. W. Hawkes (editor), Advances in Imaging and Electron Physics, volume 128, pages 205–308, Elsevier, January 2003. https://www.sciencedirect.com/science/article/pii/S1076567003800654, doi:10.1016/S1076-5670(03)80065-4

[11]

G. M. D’Ariano, M. G.A. Paris, and M. F. Sacchi, “2 Quantum Tomographic Methods”, M. Paris and J. Řeháček (editors), Quantum State Estimation, Lecture Notes in Physics, pages 7–58, Springer, Berlin, Heidelberg, 2004. https://doi.org/10.1007/978-3-540-44481-7_2, doi:10.1007/978-3-540-44481-7_2

[12]

Y. Aharonov and D. Rohrlich, Quantum Paradoxes: Quantum Theory for the Perplexed, Wiley, 1st edition, February 2005.

[13]

Y. Aharonov, D. Z. Albert, and L. Vaidman, “How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100”, Physical Review Letters, 60(14):1351–1354, April 1988. https://link.aps.org/doi/10.1103/PhysRevLett.60.1351, doi:10.1103/PhysRevLett.60.1351

[14]

A. Peres, “Quantum measurements with postselection”, Physical Review Letters, 62(19):2326–2326, May 1989. https://link.aps.org/doi/10.1103/PhysRevLett.62.2326, doi:10.1103/PhysRevLett.62.2326

[15]

A. J. Leggett, “Comment on “How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100””, Physical Review Letters, 62(19):2325–2325, May 1989. https://link.aps.org/doi/10.1103/PhysRevLett.62.2325, doi:10.1103/PhysRevLett.62.2325

[16]

Y. Aharonov and L. Vaidman, “Aharonov and Vaidman reply”, Physical Review Letters, 62(19):2327–2327, May 1989. https://link.aps.org/doi/10.1103/PhysRevLett.62.2327, doi:10.1103/PhysRevLett.62.2327

[17]

I. M. Duck, P. M. Stevenson, and E. C. G. Sudarshan, “The sense in which a “weak measurement” of a spin-1/2 particle's spin component yields a value 100”, Physical Review D, 40(6):2112–2117, September 1989. https://link.aps.org/doi/10.1103/PhysRevD.40.2112, doi:10.1103/PhysRevD.40.2112

[18]

Y. Aharonov and L. Vaidman, “Properties of a quantum system during the time interval between two measurements”, Physical Review A, 41(1):11–20, January 1990. https://link.aps.org/doi/10.1103/PhysRevA.41.11, doi:10.1103/PhysRevA.41.11

[19]

J. M. Knight and L. Vaidman, “Weak measurement of photon polarization”, Physics Letters A, 143(8):357–361, January 1990. https://www.sciencedirect.com/science/article/pii/037596019090371T, doi:10.1016/0375-9601(90)90371-T

[20]

J.g. Story, N.w.m. Ritchie, and R.g. Hulet, “Weak measurements”, Modern Physics Letters B, 05(26):1713–1725, November 1991. https://www.worldscientific.com/doi/abs/10.1142/S0217984991002069, doi:10.1142/S0217984991002069

[21]

L. M. Johansen, “Weak Measurements with Arbitrary Probe States”, Physical Review Letters, 93(12):120402, September 2004. https://link.aps.org/doi/10.1103/PhysRevLett.93.120402, doi:10.1103/PhysRevLett.93.120402

[22]

L. Vaidman, “Weak Value and Weak Measurements”, D. Greenberger, K. Hentschel, and F. Weinert (editors), Compendium of Quantum Physics, pages 840–842, Springer, Berlin, Heidelberg, 2009. https://doi.org/10.1007/978-3-540-70626-7_235, doi:10.1007/978-3-540-70626-7_235

[23]

S. Wu and K. Mølmer, “Weak measurements with a qubit meter”, Physics Letters A, 374(1):34–39, December 2009. https://www.sciencedirect.com/science/article/pii/S0375960109012882, doi:10.1016/j.physleta.2009.10.026

[24]

Y. Kedem and L. Vaidman, “Modular Values and Weak Values of Quantum Observables”, Physical Review Letters, 105(23):230401, November 2010. https://link.aps.org/doi/10.1103/PhysRevLett.105.230401, doi:10.1103/PhysRevLett.105.230401

[25]

S. Wu and Y. Li, “Weak measurements beyond the Aharonov-Albert-Vaidman formalism”, Physical Review A, 83(5):052106, May 2011. https://link.aps.org/doi/10.1103/PhysRevA.83.052106, doi:10.1103/PhysRevA.83.052106

[26]

K. Nakamura, A. Nishizawa, and M.-K. Fujimoto, “Evaluation of weak measurements to all orders”, Physical Review A, 85(1):012113, January 2012. https://link.aps.org/doi/10.1103/PhysRevA.85.012113, doi:10.1103/PhysRevA.85.012113

[27]

J. S. Lundeen and C. Bamber, “Procedure for Direct Measurement of General Quantum States Using Weak Measurement”, Physical Review Letters, 108(7):070402, February 2012. https://link.aps.org/doi/10.1103/PhysRevLett.108.070402, doi:10.1103/PhysRevLett.108.070402

[28]

S. Pang, S. Wu, and Z.-B. Chen, “Weak measurement with orthogonal preselection and postselection”, Physical Review A, 86(2):022112, August 2012. https://link.aps.org/doi/10.1103/PhysRevA.86.022112, doi:10.1103/PhysRevA.86.022112

[29]

A. G. Kofman, S. Ashhab, and F. Nori, “Nonperturbative theory of weak pre- and post-selected measurements”, Physics Reports, 520(2):43–133, November 2012. https://www.sciencedirect.com/science/article/pii/S0370157312002050, doi:10.1016/j.physrep.2012.07.001

[30]

L. G. Bishop, F. Costa, and T. C. Ralph, “Quantum state tomography on closed timelike curves using weak measurements”, Classical and Quantum Gravity, 42(4):045018, February 2025. https://dx.doi.org/10.1088/1361-6382/ada90b, doi:10.1088/1361-6382/ada90b