Fourier transform adder

Description

The version of a quantum adder presented here sums two multi-qubit integers essentially by computing the summation in Fourier space [1, 2, 3, 4, 5, 6]. This is achieved by first performing a quantum (discrete) Fourier transform on one of the encoded integers, following with a controlled-phase gate (serving the same function as an ordinary full adder in ordinary non-Fourier Hilbert space), and concluding with an inverse Fourier transform on the same integer.

Figure 21 A quantum circuit diagram of a QFT-based adder.

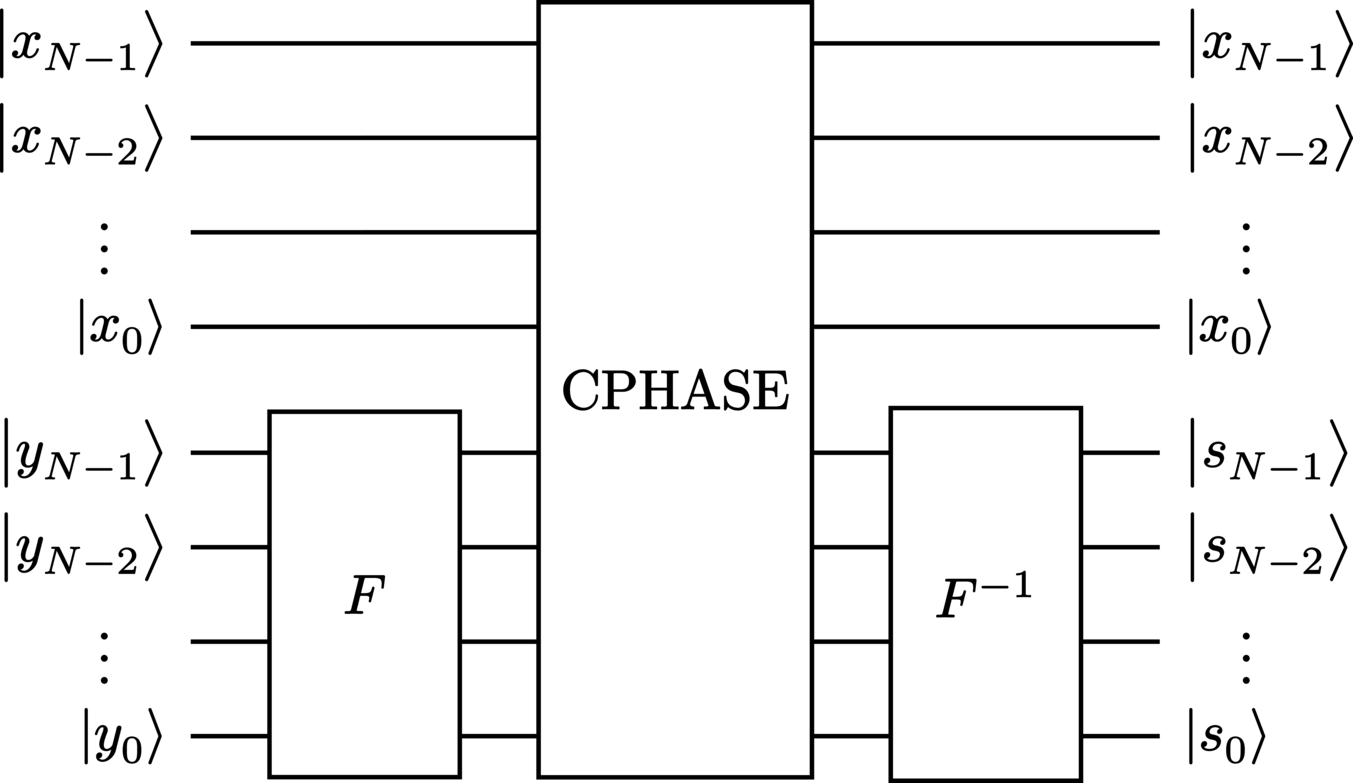
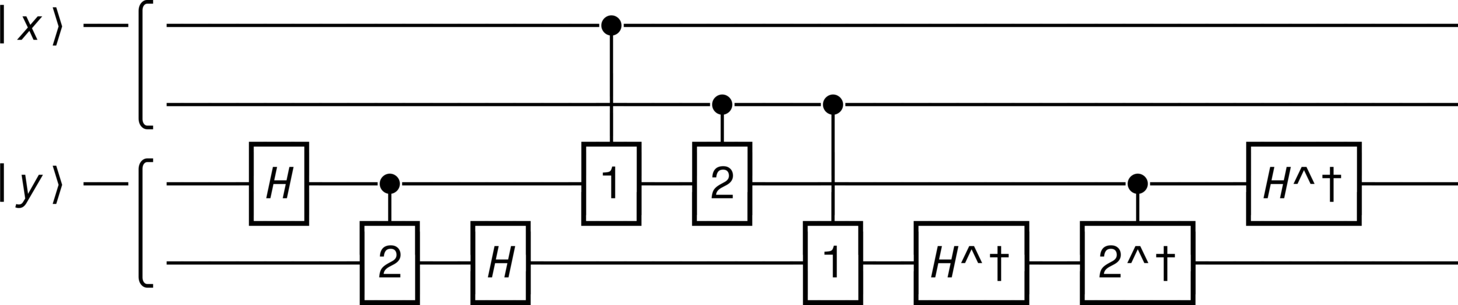
An example of this algorithm for \(3\)-qubit integers appears in Figure 22.

Figure 22 A QFT-based adder for \(3\)-qubit states.

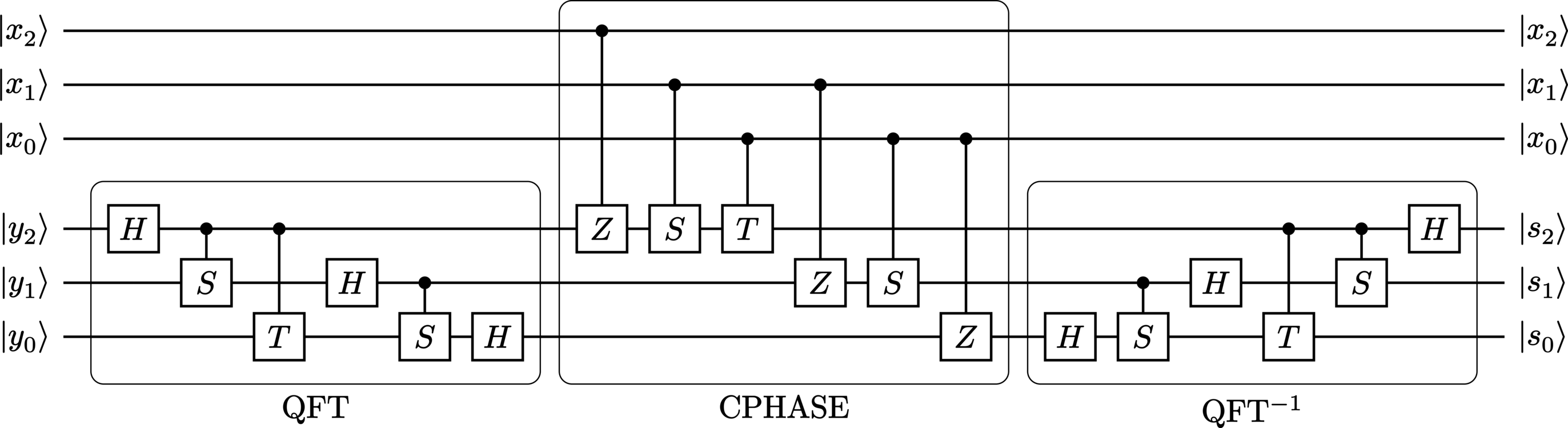
Implementation

Listing 21 /text/examples/algorithms/adder_fourier.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Hadamard, Phase, Fourier
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.utilities.helpers import flatten_list
from qhronology.mechanics.matrices import encode, decode

import sympy as sp

import time

initial_time = time.time()

augend_integer = 1
addend_integer = 1
encoding_depth = 2

# Input
augend_state = VectorState(
    spec=encode(integer=augend_integer, num_systems=encoding_depth), label="x"
)
addend_state = VectorState(
    spec=encode(integer=addend_integer, num_systems=encoding_depth), label="y"
)

QFT = []
IQFT = []
for i in range(0, encoding_depth):
    count = encoding_depth - i
    for j in range(0, count):
        if j == 0:
            QFT.append(
                Hadamard(
                    targets=[i + encoding_depth],
                    num_systems=2 * encoding_depth,
                    conjugate=False,
                    label="H",
                )
            )
            IQFT.append(
                Hadamard(
                    targets=[i + encoding_depth],
                    num_systems=2 * encoding_depth,
                    conjugate=True,
                    label="H^†",
                )
            )
        else:
            QFT.append(
                Phase(
                    targets=[i + j + encoding_depth],
                    controls=[i + encoding_depth],
                    exponent=sp.Rational(1, (2**j)),
                    num_systems=2 * encoding_depth,
                    conjugate=False,
                    label=f"{2**j}",
                    family="GATE",
                )
            )
            IQFT.append(
                Phase(
                    targets=[i + j + encoding_depth],
                    controls=[i + encoding_depth],
                    exponent=sp.Rational(1, (2**j)),
                    num_systems=2 * encoding_depth,
                    conjugate=True,
                    label=f"{2**j}^†",
                    family="GATE",
                )
            )

IQFT = IQFT[::-1]

CPHASE = []
for i in range(0, encoding_depth):
    count = encoding_depth - i
    for j in range(0, count):
        CPHASE.append(
            Phase(
                targets=[i + encoding_depth],
                controls=[j + i],
                exponent=sp.Rational(1, (2**j)),
                num_systems=2 * encoding_depth,
                label=f"{2**j}",
                family="GATE",
            )
        )

gates = flatten_list(QFT + CPHASE + IQFT)

# Circuit
adder = QuantumCircuit(inputs=[augend_state, addend_state], gates=gates)
adder.diagram()

# Output
sum_registers = [(i + encoding_depth) for i in range(0, encoding_depth)]
sum_registers_complement = [
    i for i in range(0, 2 * encoding_depth) if i not in sum_registers
]
sum_state = adder.state(label="s", traces=sum_registers_complement)
sum_integer = decode(sum_state.output())

# Results
augend_state.print()
addend_state.print()
sum_state.print()

final_time = time.time()
computation = f"Computation: {augend_integer} + {addend_integer} = {sum_integer}"
duration = f"Duration: {sp.N(final_time - initial_time,8).round(3)} seconds"
print(computation)
print(duration)

Output

Diagram

>>> adder.diagram()

States

>>> augend_state.print()
|x⟩ = |0,1⟩

>>> addend_state.print()
|y⟩ = |0,1⟩

>>> sum_state.print()
s = |1,0⟩⟨1,0|

Results

>>> print(computation)
Computation: 1 + 1 = 2

>>> print(duration)
Duration: 0.283 seconds

As both the number of qubits and the circuit depth (number of gates) of the quantum Fourier adder are significantly smaller than any of the other quantum adder algorithms, we appropriately find that its operation is computationally much faster.

References

[1]

T. G. Draper, “Addition on a Quantum Computer”, August 2000. http://arxiv.org/abs/quant-ph/0008033, doi:10.48550/arXiv.quant-ph/0008033

[2]

L. Ruiz-Perez and J. C. Garcia-Escartin, “Quantum arithmetic with the quantum Fourier transform”, Quantum Information Processing, 16(6):152, April 2017. https://doi.org/10.1007/s11128-017-1603-1, doi:10.1007/s11128-017-1603-1

[3]

E. Şahin, “Quantum arithmetic operations based on quantum fourier transform on signed integers”, International Journal of Quantum Information, 18(06):2050035, September 2020. https://www.worldscientific.com/doi/abs/10.1142/S0219749920500355, doi:10.1142/S0219749920500355

[4]

R. Seidel, N. Tcholtchev, S. Bock, C. K.-U. Becker, and M. Hauswirth, “Efficient Floating Point Arithmetic for Quantum Computers”, IEEE Access, 10:72400–72415, 2022. https://ieeexplore.ieee.org/document/9815035, doi:10.1109/ACCESS.2022.3188251

[5]

P. Atchade-Adelomou and S. Gonzalez, “Efficient Quantum Modular Arithmetics for the ISQ Era”, November 2023. http://arxiv.org/abs/2311.08555, doi:10.48550/arXiv.2311.08555

[6]

S. Wang, X. Li, W. J. B. Lee, S. Deb, E. Lim, and A. Chattopadhyay, “A comprehensive study of quantum arithmetic circuits”, Philosophical Transactions A, January 2025. https://royalsocietypublishing.org/doi/10.1098/rsta.2023.0392, doi:10.1098/rsta.2023.0392