PSWAP (power-SWAP)

Description

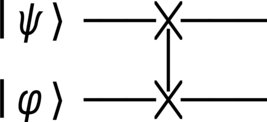
Exponentiation of the SWAP gate produces an interesting interaction (PSWAP) between its input systems: the degree to which their states’ values are exchanged depends entirely on the power to which the SWAP gate is taken. This effect means that the PSWAP gate is useful for modelling interesting physical phenomena such as probabilistic scattering, where the power parameter of the gate is analogous to the interaction chance of two particles in a scattering experiment. For even powers, no SWAP occurs, while for odd powers, a SWAP does occur. Non-integer values of the power therefore smoothly interpolate between these two outcomes in the form of a (weighted) quantum superposition of them. Figure 24 depicts a simple PSWAP interaction.

Figure 24 A PSWAP gate (with power \(p\)).

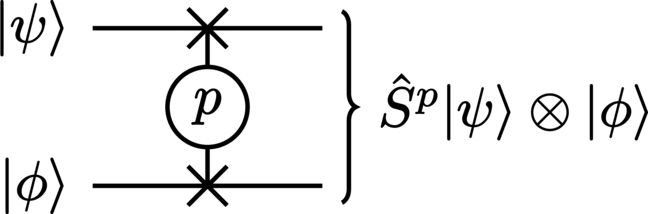
Implementation

Listing 23 /text/examples/algorithms/pswap.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Swap
from qhronology.quantum.circuits import QuantumCircuit

# Input
psi = VectorState(
    spec=[("a", [0]), ("b", [1])],
    symbols={"a": {"complex": True}, "b": {"complex": True}},
    conditions=[("a*conjugate(a) + b*conjugate(b)", "1")],
    dim=2,
    norm=1,
    label="ψ",
)
phi = VectorState(
    spec=[("c", [0]), ("d", [1])],
    symbols={"c": {"complex": True}, "d": {"complex": True}},
    conditions=[("c*conjugate(c) + d*conjugate(d)", "1")],
    dim=2,
    norm=1,
    label="φ",
)

# Gate
S = Swap(
    targets=[0, 1],
    num_systems=2,
    exponent="p",
    symbols={"p": {"real": True}},
    notation="S^p",
)

# Circuit
pswap = QuantumCircuit(inputs=[psi, phi], gates=[S])
pswap.diagram()

# Output
input_state = QuantumCircuit(inputs=[psi, phi]).state(label="ψ,φ")
output_state = pswap.state(label="(ψ,φ)'")

# Results
print(repr(pswap.gate()))
input_state.print()
output_state.print()

Output

Diagram

>>> pswap.diagram()

Gate

>>> print(repr(pswap.gate()))
Matrix([
[1,                   0,                   0, 0],
[0, exp(I*pi*p)/2 + 1/2, 1/2 - exp(I*pi*p)/2, 0],
[0, 1/2 - exp(I*pi*p)/2, exp(I*pi*p)/2 + 1/2, 0],
[0,                   0,                   0, 1]])

States

>>> input_state.print()
|ψ,φ⟩ = a*c|0,0⟩ + a*d|0,1⟩ + b*c|1,0⟩ + b*d|1,1⟩

>>> output_state.print()
|(ψ,φ)'⟩ = a*c|0,0⟩ + (a*d*(exp(I*pi*p)/2 + 1/2) + b*c*(1/2 - exp(I*pi*p)/2))|0,1⟩ + (a*d*(1/2 - exp(I*pi*p)/2) + b*c*(exp(I*pi*p)/2 + 1/2))|1,0⟩ + b*d|1,1⟩