Unproven-theorem paradox

Description

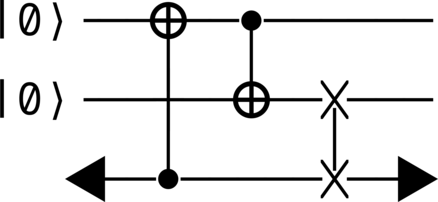
The unproven-theorem paradox [4, 1, 3] (depicted in Figure 28) is, as we shall see, not as straightforward as other temporal paradoxes. Here, the CR system is comprised of two subsystems: the first (upper) is the book, and the second (lower) is the mathematician.

Figure 28 A quantum model of the unproven-theorem paradox under the D-CTCs prescription.

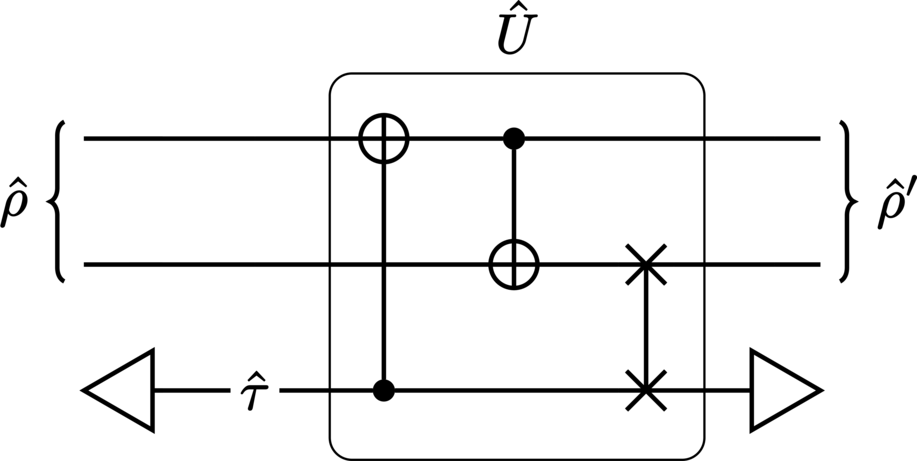
Described by the unitary

(387)\[\Unitary = \Swap^{1,2} \cdot \Control^0 \NOT^1 \cdot \Control^2 \NOT^0,\]

the unproven-theorem paradox encapsulates the scenario in which the proof of a theorem that a mathematician reads in the past is the very same proof which they write down in the future book (with the book having travelled back in time). We therefore denote the absence and presence of the proof in each subsystem intuitively by \(\ket{0}\) and \(\ket{1}\), respectively. Under this interpretation, when the mathematician and/or the book are in the state \(\ket{1}\), they possess a “correct” proof, while being in the state \(\ket{0}\) means that they do not. (Alternatively, one can think of these qubit levels as denoting different answers to some problem the mathematician is working on. They can then encode their proof of some theorem into an \(\Number\)-bit binary string by using \(\Number\) copies of the circuit [1].) Thus, the CR input state

(388)\[\StateCR = \ket{0}\bra{0}\otimes\ket{0}\bra{0}\]

describes the situation in which both the book and mathematician do not initially possess the proof.

Solutions

D-CTCs

To find the D-CTC solutions, we first compute the standard evolution with the CR input state (388),

(389)\[\begin{split}\begin{aligned} \MapGeneral_{\Unitary} [\StateCR \otimes \StateCV] &= \Unitary \bigl(\ket{0}\bra{0}\otimes\ket{0}\bra{0} \otimes \StateCV\bigr) \Unitary^\dagger \\ &= \Swap^{1,2} \cdot \Control^0 \NOT^1 \cdot \Control^2 \NOT^0 \bigl(\ket{0}\bra{0}\otimes\ket{0}\bra{0} \otimes \StateCV\bigr) \Control^2 \NOT^{\dagger 0} \cdot \Control^0 \NOT^{\dagger 1} \cdot \Swap^{\dagger 1,2} \\ &= \Swap^{1,2} \cdot \Control^0 \NOT^1 \bigl(\ket{0}\bra{0}\otimes\ket{0}\bra{0} \otimes \ket{0}\bra{0}\StateCV\ket{0}\bra{0} \\ & \qquad\qquad\qquad\;\; + \ket{0}\bra{1}\otimes\ket{0}\bra{0} \otimes \ket{0}\bra{0}\StateCV\ket{1}\bra{1} \\ & \qquad\qquad\qquad\;\; + \ket{1}\bra{0}\otimes\ket{0}\bra{0} \otimes \ket{1}\bra{1}\StateCV\ket{0}\bra{0} \\ & \qquad\qquad\qquad\;\; + \ket{1}\bra{1}\otimes\ket{0}\bra{0} \otimes \ket{1}\bra{1}\StateCV\ket{1}\bra{1}\bigr) \Control^0 \NOT^{\dagger 1} \cdot \Swap^{\dagger 1,2} \\ &= \Swap^{1,2} \bigl(\ket{0}\bra{0}\otimes\ket{0}\bra{0} \otimes \ket{0}\bra{0}\StateCV\ket{0}\bra{0} \\ & \qquad\quad\;\; + \ket{0}\bra{1}\otimes\ket{0}\bra{1} \otimes \ket{0}\bra{0}\StateCV\ket{1}\bra{1} \\ & \qquad\quad\;\; + \ket{1}\bra{0}\otimes\ket{1}\bra{0} \otimes \ket{1}\bra{1}\StateCV\ket{0}\bra{0} \\ & \qquad\quad\;\; + \ket{1}\bra{1}\otimes\ket{1}\bra{1} \otimes \ket{1}\bra{1}\StateCV\ket{1}\bra{1}\bigr) \Swap^{\dagger 1,2} \\ &= \ket{0}\bra{0} \otimes \ket{0}\bra{0}\StateCV\ket{0}\bra{0} \otimes \ket{0}\bra{0} \\ & \quad\; + \ket{0}\bra{1} \otimes \ket{0}\bra{0}\StateCV\ket{1}\bra{1} \otimes \ket{0}\bra{1} \\ & \quad\; + \ket{1}\bra{0} \otimes \ket{1}\bra{1}\StateCV\ket{0}\bra{0} \otimes \ket{1}\bra{0} \\ & \quad\; + \ket{1}\bra{1} \otimes \ket{1}\bra{1}\StateCV\ket{1}\bra{1} \otimes \ket{1}\bra{1}. \end{aligned}\end{split}\]

Subsequently tracing out the CR system (subsystems \(0\) and \(1\)) yields the CV map,

(390)\[\begin{split}\begin{aligned} \MapDCTCsCV_{\Unitary} [\StateCR,\StateCV] &= \trace_{0, 1} \bigl[\Unitary \bigl(\ket{0}\bra{0} \otimes \ket{0}\bra{0} \otimes \StateCV\bigr) \Unitary^\dagger\bigr] \\ &= \bra{0}\StateCV\ket{0} \cdot \ket{0}\bra{0} + \bra{1}\StateCV\ket{1} \cdot \ket{1}\bra{1}, \end{aligned}\end{split}\]

while tracing out the CV system (subsystem \(2\)) gives the CR map,

(391)\[\begin{split}\begin{aligned} \MapDCTCsCR_{\Unitary} [\StateCR,\StateCV] &= \trace_{2} \bigl[\Unitary \bigl(\ket{0}\bra{0} \otimes \ket{0}\bra{0} \otimes \StateCV\bigr) \Unitary^\dagger\bigr] \\ &= \bra{0}\StateCV\ket{0} \cdot \ket{0}\bra{0} \otimes \ket{0}\bra{0} + \bra{1}\StateCV\ket{1} \cdot \ket{1}\bra{1} \otimes \ket{1}\bra{1}. \end{aligned}\end{split}\]

According to D-CTCs, solutions to the CV map are given as fixed points, which we can calculate as any density matrix \(\StateCV\) that satisfies

(392)\[\StateCV = \bra{0}\StateCV\ket{0} \cdot \ket{0}\bra{0} + \bra{1}\StateCV\ket{1} \cdot \ket{1}\bra{1}.\]

Comparing the terms (entries) of the density matrix then gives the simultaneous equations

(393)\[\begin{split}\begin{aligned} \bra{0}\StateCV\ket{0} &= \bra{0}\StateCV\ket{0}, \\ \bra{1}\StateCV\ket{0} &= 0, \\ \bra{0}\StateCV\ket{1} &= 0, \\ \bra{1}\StateCV\ket{1} &= \bra{1}\StateCV\ket{1}. \end{aligned}\end{split}\]

These equations, along with the trace condition

(394)\[\trace[\StateCV] = \bra{0}\StateCV\ket{0} + \bra{1}\StateCV\ket{1} = 1,\]

(which describes the expectation that any CV state is normalized), are solved when

(395)\[\bra{1}\StateCV\ket{1} = 1 - \bra{0}\StateCV\ket{0},\]

with all other terms equal to zero. This expresses a continuum of solutions that can be expressed in a parametrized form, with one such way being the natural choice

(396)\[\begin{split}\begin{aligned} \bra{0}\StateCV\ket{0} &= \ParameterFree, \\ \bra{1}\StateCV\ket{1} &= 1 - \ParameterFree. \end{aligned}\end{split}\]

Here, we introduced the free parameter \(0 \leq \ParameterFree \leq 1\), which encapsulates the notion of (infinite) multiplicity in the solutions to the D-CTC CV map. With this parametrization, the corresponding CV state can be written as

(397)\[\StateCV_{\MapDCTCsCR} = \ParameterFree\ket{0}\bra{0} + (1 - \ParameterFree)\ket{1}\bra{1}.\]

For the CR solution, we simply use the calculated CV state in our computation of the CR map, and accordingly find

(398)\[\StateCR_{\MapDCTCsCR} = \ParameterFree\ket{0}\bra{0}\otimes\ket{0}\bra{0} + (1 - \ParameterFree)\ket{1}\bra{1}\otimes\ket{1}\bra{1}.\]

P-CTCs

To compute the P-CTC CR solution, we first calculate the P-CTC operator,

(399)\[\begin{split}\begin{aligned} \OperatorPCTC &\equiv \trace_\CV[\Unitary] \\ &= \trace_2\bigl[\Swap^{1,2} \cdot \Control^0 \NOT^1 \cdot \Control^2 \NOT^0\bigr] \\ &= \trace_2\bigl[\Swap^{1,2} \cdot \bigl(\ket{0}\bra{0} \otimes \Identity \otimes \Identity + \ket{1}\bra{1} \otimes \Pauli_x \otimes \Identity\bigr) \cdot \bigl(\Identity \otimes \Identity \otimes \ket{0}\bra{0} + \Pauli_x \otimes \Identity \otimes \ket{1}\bra{1}\bigr)\bigr] \\ &= \trace_2\bigl[\Swap^{1,2} \cdot \bigl(\ket{0}\bra{0} \otimes \Identity \otimes \ket{0}\bra{0} \\ &\qquad\qquad\quad\;\;\; + \ket{1}\bra{1} \otimes \Pauli_x \otimes \ket{0}\bra{0} \\ &\qquad\qquad\quad\;\;\; + \ket{0}\bra{1} \otimes \Identity \otimes \ket{1}\bra{1} \\ &\qquad\qquad\quad\;\;\; + \ket{1}\bra{0} \otimes \Pauli_x \otimes \ket{1}\bra{1}\bigr)\bigr] \\ &= \trace_2\bigl[\Swap^{1,2} \cdot \bigl(\ket{0}\bra{0} \otimes \ket{0}\bra{0} \otimes \ket{0}\bra{0} \\ &\qquad\qquad\quad\;\;\; + \ket{0}\bra{0} \otimes \ket{1}\bra{1} \otimes \ket{0}\bra{0} \\ &\qquad\qquad\quad\;\;\; + \ket{1}\bra{1} \otimes \ket{0}\bra{1} \otimes \ket{0}\bra{0} \\ &\qquad\qquad\quad\;\;\; + \ket{1}\bra{1} \otimes \ket{1}\bra{0} \otimes \ket{0}\bra{0} \\ &\qquad\qquad\quad\;\;\; + \ket{0}\bra{1} \otimes \ket{0}\bra{0} \otimes \ket{1}\bra{1} \\ &\qquad\qquad\quad\;\;\; + \ket{0}\bra{1} \otimes \ket{1}\bra{1} \otimes \ket{1}\bra{1} \\ &\qquad\qquad\quad\;\;\; + \ket{1}\bra{0} \otimes \ket{0}\bra{1} \otimes \ket{1}\bra{1} \\ &\qquad\qquad\quad\;\;\; + \ket{1}\bra{0} \otimes \ket{1}\bra{0} \otimes \ket{1}\bra{1}\bigr)\bigr] \\ &= \trace_2\bigl[\ket{0}\bra{0} \otimes \ket{0}\bra{0} \otimes \ket{0}\bra{0} \\ &\qquad\quad + \ket{0}\bra{0} \otimes \ket{0}\bra{1} \otimes \ket{1}\bra{0} \\ &\qquad\quad + \ket{1}\bra{1} \otimes \ket{0}\bra{1} \otimes \ket{0}\bra{0} \\ &\qquad\quad + \ket{1}\bra{1} \otimes \ket{0}\bra{0} \otimes \ket{1}\bra{0} \\ &\qquad\quad + \ket{0}\bra{1} \otimes \ket{1}\bra{0} \otimes \ket{0}\bra{1} \\ &\qquad\quad + \ket{0}\bra{1} \otimes \ket{1}\bra{1} \otimes \ket{1}\bra{1} \\ &\qquad\quad + \ket{1}\bra{0} \otimes \ket{1}\bra{1} \otimes \ket{0}\bra{1} \\ &\qquad\quad + \ket{1}\bra{0} \otimes \ket{1}\bra{0} \otimes \ket{1}\bra{1}\bigr] \\ &= \ket{0}\bra{0} \otimes \ket{0}\bra{0} + \ket{1}\bra{1} \otimes \ket{0}\bra{1} + \ket{0}\bra{1} \otimes \ket{1}\bra{1} + \ket{1}\bra{0} \otimes \ket{1}\bra{0} \\ &= \sqrt{2}\bigl(\ket{\Phi^+}\bra{0,0} + \ket{\Psi^+}\bra{1,1}\bigr). \end{aligned}\end{split}\]

With this, we can easily determine the P-CTC CR state (corresponding to the input state (388)) via its definition (250),

(400)\[\begin{split}\begin{aligned} \StateCR_\MapPCTCsCR &= \MapPCTCsCR_{\Unitary} [\StateCR ] \\ &= \frac{\OperatorPCTC \ket{0}\bra{0} \otimes \ket{0}\bra{0} \OperatorPCTC^\dagger}{\trace\bigr[\OperatorPCTC \ket{0}\bra{0} \otimes \ket{0}\bra{0} \OperatorPCTC^\dagger\bigr]} \\ &= \ket{\Phi^+}\bra{\Phi^+}. \end{aligned}\end{split}\]

Lastly, using the expression (253), we can compute the P-CTC CV state (via weak-measurement quantum state tomography) to be

(401)\[\begin{split}\begin{aligned} \StateCV_\MapPCTCsCR &= \frac{1}{2}\Identity \\ &= \frac{1}{2}\bigl(\ket{0}\bra{0} + \ket{1}\bra{1}\bigr). \end{aligned}\end{split}\]

Observe that the D-CTC resolution (397) turns out not to be unique (with free parameter \(\ParameterFree\)), while the P-CTC CR state (400) is. The interpretation of these solutions is that, according the P-CTCs, the mathematician and the book will be in a superposition of both possessing the proof and neither possessing it, while according to D-CTCs, the two parties will be in a parametrized mixture of such possibilities. Additionally, it is easy to see that the P-CTC CV state is the maximally entropic form of its D-CTC counterpart, which means that the ECP end-state evolution (the “correct” D-CTC fixed point which resolves the uniqueness ambiguity) in this case (398) coincidentally is exactly the P-CTC CV solution (401).

Implementation

Listing 28 /text/examples/ctcs/unproven.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not, Swap
from qhronology.quantum.prescriptions import QuantumCTC, DCTC, PCTC

# Input
mathematician_state = VectorState(spec=[(1, [0])], label="0")
book_state = VectorState(spec=[(1, [0])], label="0")

# Gates
NIC = Not(targets=[0], controls=[2], num_systems=3)
CNI = Not(targets=[1], controls=[0], num_systems=3)
IS = Swap(targets=[1, 2], num_systems=3)

# CTC
unproven = QuantumCTC(
    inputs=[mathematician_state, book_state],
    gates=[NIC, CNI, IS],
    systems_respecting=[0, 1],
)
unproven.diagram()

# Output
# D-CTCs
unproven_DCTC = DCTC(circuit=unproven)
unproven_DCTC_respecting = unproven_DCTC.state_respecting(norm=1, label="ρ_D")
unproven_DCTC_violating = unproven_DCTC.state_violating(norm=1, label="τ_D")

# P-CTCs
unproven_PCTC = PCTC(circuit=unproven)
unproven_PCTC_respecting = unproven_PCTC.state_respecting(norm=1, label="ψ_P")
unproven_PCTC_violating = unproven_PCTC.state_violating(norm=1, label="τ_P")

# Results
unproven_DCTC_respecting.print()
unproven_DCTC_violating.print()
unproven_PCTC_respecting.print()
unproven_PCTC_violating.print()

Output

Diagram

>>> unproven.diagram()

States

>>> unproven_DCTC_respecting.print()
ρ_D = g|0,0⟩⟨0,0| + (1 - g)|1,1⟩⟨1,1|

>>> unproven_DCTC_violating.print()
τ_D = g|0⟩⟨0| + (1 - g)|1⟩⟨1|

>>> unproven_PCTC_respecting.print()
|ψ_P⟩ = sqrt(2)/2|0,0⟩ + sqrt(2)/2|1,1⟩

>>> unproven_PCTC_violating.print()
τ_P = 1/2|0⟩⟨0| + 1/2|1⟩⟨1|

References

[1] (1,2)

J.-M. A. Allen, “Treating time travel quantum mechanically”, Physical Review A, 90(4):042107, October 2014. https://link.aps.org/doi/10.1103/PhysRevA.90.042107, doi:10.1103/PhysRevA.90.042107

[2]

S. Lloyd, L. Maccone, R. Garcia-Patron, V. Giovannetti, Y. Shikano, S. Pirandola, L. A. Rozema, A. Darabi, Y. Soudagar, L. K. Shalm, and A. M. Steinberg, “Closed Timelike Curves via Postselection: Theory and Experimental Test of Consistency”, Physical Review Letters, 106(4):040403, January 2011. https://link.aps.org/doi/10.1103/PhysRevLett.106.040403, doi:10.1103/PhysRevLett.106.040403

[3]

D. Deutsch, “Quantum mechanics near closed timelike lines”, Physical Review D, 44(10):3197–3217, November 1991. https://link.aps.org/doi/10.1103/PhysRevD.44.3197, doi:10.1103/PhysRevD.44.3197