Generation of a W state

Description

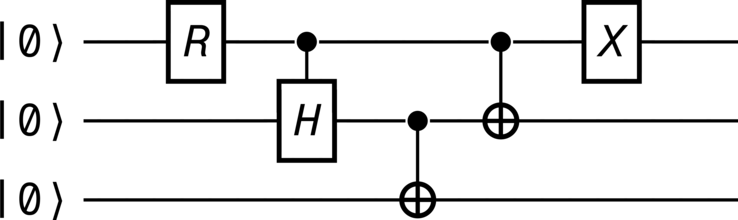
The circuit in Figure 11 illustrates an algorithm for the generation of a W state (170) from primitive \(\ket{0}\) states.

Figure 11 Generation of a W state.

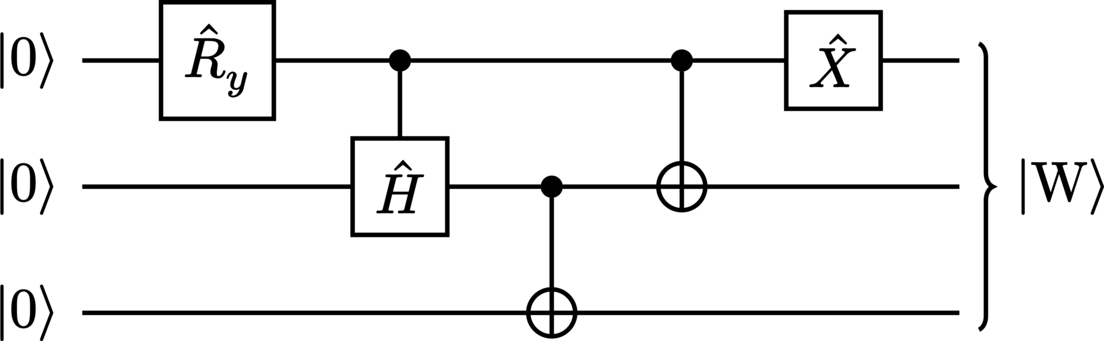
The complete unitary transformation described by this circuit is the product

(329)\[\Unitary = \NOT^0 \cdot \Control^0 \NOT^1 \cdot \Control^1 \NOT^2 \cdot \Control^0 \Hadamard^1 \cdot \Rotation_{y}^0(\theta)\]

where the \(y\)-rotation angle is \(\theta = 2 \arccos\left(\tfrac{1}{\sqrt{3}}\right)\).

Implementation

Listing 11 /text/examples/algorithms/generation_w.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Rotation, Hadamard, Not, Pauli
from qhronology.quantum.circuits import QuantumCircuit

# Input
zero_state = VectorState(spec=[(1, [0])], label="0")

# Gates
RII = Rotation(axis=2, angle="2*acos(1/sqrt(3))", targets=[0], num_systems=3, label="R")
CHI = Hadamard(targets=[1], controls=[0], num_systems=3)
ICN = Not(targets=[2], controls=[1], num_systems=3)
CNI = Not(targets=[1], controls=[0], num_systems=3)
XII = Pauli(index=1, targets=[0], num_systems=3)

# Circuit
generator = QuantumCircuit(
    inputs=[zero_state, zero_state, zero_state], gates=[RII, CHI, ICN, CNI, XII]
)
generator.diagram()

# Output
w_state = generator.state(label="W")

# Results
w_state.print()

Output

Diagram

>>> generator.diagram()

State

>>> w_state.print()
|W⟩ = sqrt(3)/3|0,0,1⟩ + sqrt(3)/3|0,1,0⟩ + sqrt(3)/3|1,0,0⟩