Manual P-CTC#

Description#

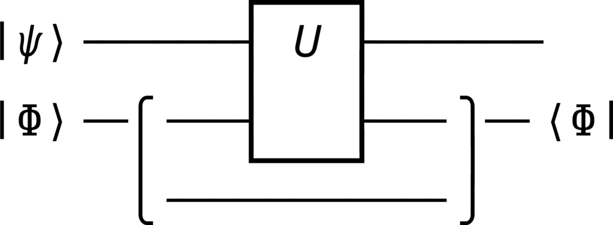
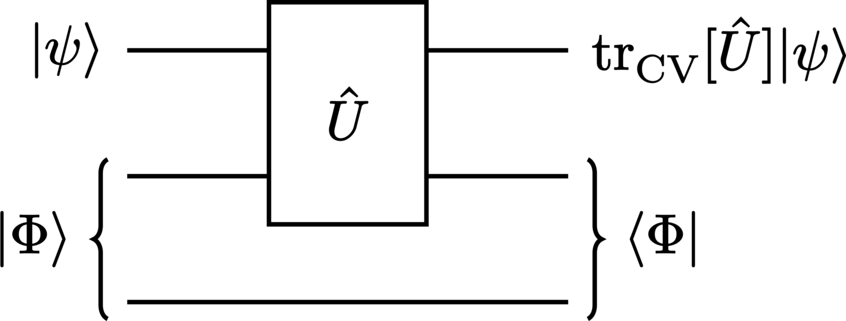
This example merely serves as a proof of the P-CTC prescription (for qubits). This is achieved by explicitly performing the Bell state preselection and postselection, and subsequently comparing the output to the prescription’s CR map.

A quantum circuit diagram of the P-CTC algorithm with explicit preselection and postselection.
A quantum circuit diagram of the P-CTC algorithm with explicit preselection and postselection.

Implementation#

Listing 30 /text/examples/ctcs/postselected.py#
from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import QuantumGate
from qhronology.quantum.circuits import QuantumCircuit

from qhronology.quantum.prescriptions import pctc_respecting

import sympy as sp

# Input
rho = sp.MatrixSymbol("ρ", 2, 2).as_mutable()
unitary = sp.MatrixSymbol("U", 4, 4).as_mutable()

input_state = VectorState(spec=[("a", [0]), ("b", [1])], label="ψ")
bell_state = VectorState(spec=[(1, [0, 0]), (1, [1, 1])], norm=1, label="Φ")

# Gate
UI = QuantumGate(spec=unitary, targets=[0, 1], num_systems=3, label="U")

# Circuit
postselected_teleportation = QuantumCircuit(
    inputs=[input_state, bell_state], gates=[UI], postselections=[(bell_state, [1, 2])]
)
postselected_teleportation.diagram(pad=(1, 0), sep=(2, 1), force_separation=True)

# Output
# Manual P-CTC
output_state = postselected_teleportation.state(label="ψ'")
output_state.apply(sp.factor)

# P-CTC prescription
spec = pctc_respecting(
    input_respecting=input_state,
    gate=unitary,
    systems_respecting=[0],
    systems_violating=[1],
)
pctc_output = VectorState(spec=spec, label="ψ_P")
pctc_output.coefficient(sp.Rational(1, 2))  # Manually renormalize
pctc_output.apply(sp.factor)

# Results
input_state.print()
output_state.print()
pctc_output.print()

Output#

Diagram#

>>> postselected_teleportation.diagram(pad=(1, 0), sep=(1, 1), force_separation=True)

States#

>>> input_state.print()
|ψ⟩ = a|0⟩ + b|1⟩

>>> output_state.print()
|ψ'⟩ = (a*U[0, 0] + a*U[1, 1] + b*U[0, 2] + b*U[1, 3])/2|0⟩ + (a*U[2, 0] + a*U[3, 1] + b*U[2, 2] + b*U[3, 3])/2|1⟩

>>> pctc_output.print()
|ψ_P⟩ = (a*U[0, 0] + a*U[1, 1] + b*U[0, 2] + b*U[1, 3])/2|0⟩ + (a*U[2, 0] + a*U[3, 1] + b*U[2, 2] + b*U[3, 3])/2|1⟩

Results#

>>> output_state.distance(pctc_output)
0