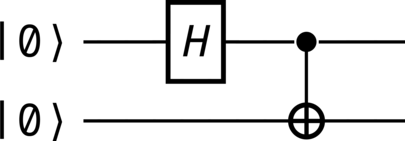
Generation of a Bell state

Description

The circuit in Figure 8 illustrates an algorithm for the generation of a Bell state (168) from primitive \(\ket{0}\) states.

Figure 8 Generation of a Bell state.

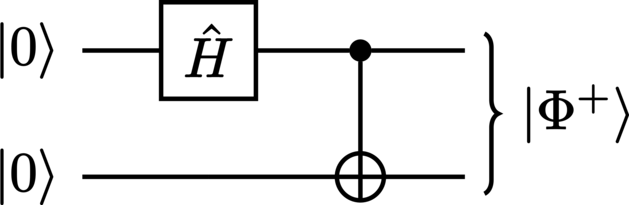
The complete unitary transformation described by this circuit is the product

(325)\[\Unitary = \Control^0 \NOT^1 \cdot \Hadamard^0.\]

Implementation

Listing 8 /text/examples/algorithms/generation_bell.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Hadamard, Not
from qhronology.quantum.circuits import QuantumCircuit

# Input
zero_state = VectorState(spec=[(1, [0])], label="0")

# Gates
HI = Hadamard(targets=[0], num_systems=2)
CN = Not(targets=[1], controls=[0], num_systems=2)

# Circuit
generator = QuantumCircuit(inputs=[zero_state, zero_state], gates=[HI, CN])
generator.diagram()

# Output
phi_plus = generator.state(label="Φ+")

# Results
phi_plus.print()

Output

Diagram

>>> generator.diagram()

State

>>> phi_plus.print()
|Φ+⟩ = sqrt(2)/2|0,0⟩ + sqrt(2)/2|1,1⟩