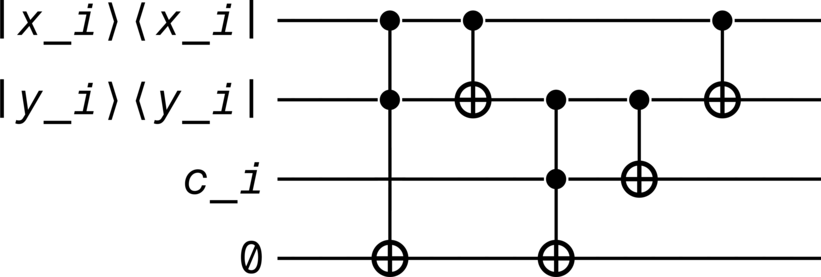
Ripple-carry adder (iterative)

Description

This example builds upon the four-qubit ripple-carry adder in Ripple-carry adder. The implementation here simplifies the algorithm by instead applying copies of the circuit successively to a tetrapartite input state, which is a composition of the augend, addend, carry, and zero states. As a result, the sequence of trace operations (necessary to isolate the output sum and carry states) mixes the pure (vector) input composition, thereby destroying linearity of the evolution in the input states. This means that only mixed states for each qubit in the output sum state can be recovered, and so we can only sum single integers, not superpositions of integers. However, keeping the Hilbert space to a smaller total dimensionality at any one time makes the computations much faster, and so we can work with significantly larger integers.

Figure 19 One iteration of a multi-qubit quantum ripple-carry adder.

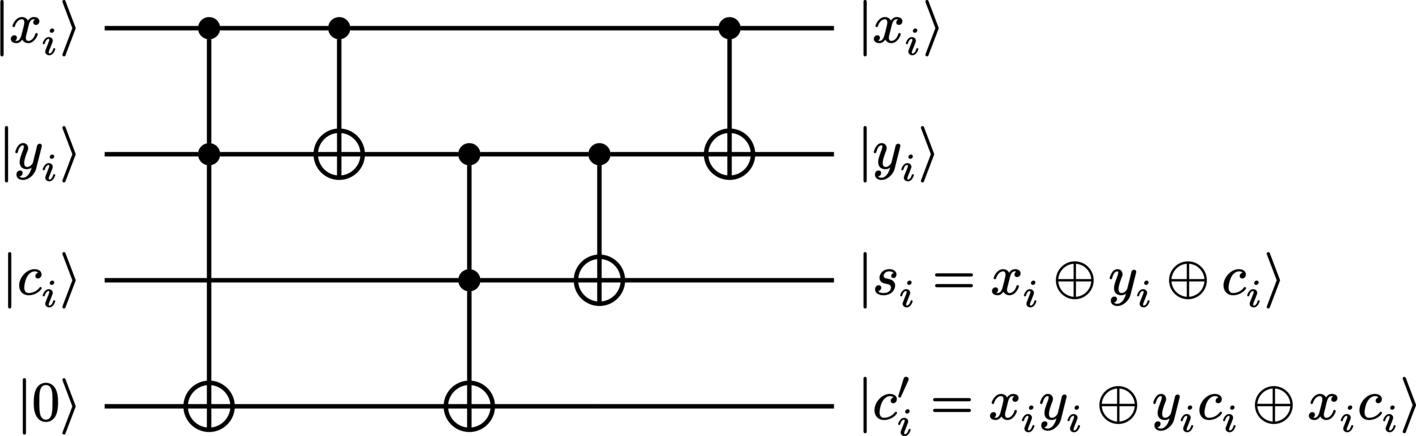
Implementation

In this example, each qubit in the uppermost set on the diagram corresponds to the leftmost (most-significant) qubit in their respective encoded state, while each qubit in the lowermost set similarly corresponds to the rightmost (least-significant) qubit.

Listing 19 /text/examples/algorithms/adder_ripple_iterative.py

from qhronology.quantum.states import QuantumState, VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.mechanics.matrices import encode, decode

import sympy as sp
from sympy.physics.quantum import TensorProduct

import time

initial_time = time.time()

augend_integer = 31
addend_integer = 217
encoding_depth = 8

# Input
augend_state = VectorState(
    spec=encode(integer=augend_integer, num_systems=encoding_depth), label="x_i"
)
addend_state = VectorState(
    spec=encode(integer=addend_integer, num_systems=encoding_depth), label="y_i"
)
carry_state = VectorState(spec=encode(0, 1), label="c_i")
zero_state = VectorState(spec=encode(0, 1), notation="0")

# Gates
CCIN = Not(targets=[3], controls=[0, 1], num_systems=4)
CNII = Not(targets=[1], controls=[0], num_systems=4)
ICCN = Not(targets=[3], controls=[1, 2], num_systems=4)
ICNI = Not(targets=[2], controls=[1], num_systems=4)

# Circuits
sum_qubits = []
for i in range(encoding_depth - 1, -1, -1):
    target_bit = i
    complement_bits = [n for n in range(0, encoding_depth) if n != target_bit]

    augend_state.reset()
    addend_state.reset()

    augend_state.partial_trace(complement_bits)
    addend_state.partial_trace(complement_bits)

    adder = QuantumCircuit(
        inputs=[augend_state, addend_state, carry_state, zero_state],
        gates=[CCIN, CNII, ICCN, ICNI, CNII],
    )

    sum_qubit = adder.state(label="s", traces=[0, 1, 3])
    carry_state = adder.state(label="c_i", traces=[0, 1, 2])
    sum_qubits = [sum_qubit.output()] + sum_qubits

adder.diagram()

# Output
sum_state = QuantumState(spec=sp.Matrix(TensorProduct(*sum_qubits)), label="s")
sum_integer = decode(sum_state.output())
sum_state = VectorState(spec=encode(sum_integer), label="s")

augend_state.reset()
addend_state.reset()

augend_state.label = "x"
addend_state.label = "y"

# Results
augend_state.print()
addend_state.print()
sum_state.print()

final_time = time.time()
computation = f"Computation: {augend_integer} + {addend_integer} = {sum_integer}"
duration = f"Duration: {sp.N(final_time - initial_time,8).round(3)} seconds"
print(computation)
print(duration)

Output

Diagram

>>> adder.diagram()

States

>>> augend_state.print()
|x⟩ = |0,0,0,1,1,1,1,1⟩

>>> addend_state.print()
|y⟩ = |1,1,0,1,1,0,0,1⟩

>>> sum_state.print()
|s⟩ = |1,1,1,1,1,0,0,0⟩

Results

>>> print(computation)
Computation: 31 + 217 = 248

>>> print(duration)
Duration: 3.264 seconds

Much faster and for much larger numbers than the linear implementation in Ripple-carry adder.