Half adder#

Description#

An adder is a circuit that sums the values of two quantum vector states in some basis. For instance, this could be the states \(\ket{x}\) and \(\ket{y}\) in a \(\Dimension\)-dimensional number basis \(\{\ket{n}\}_{n=0}^{\Dimension - 1}\). As described in CNOT (controlled-NOT), this can be accomplished with just a CNOT (controlled-NOT) gate, which produces the sum state \(\ket{x \oplus y}\).

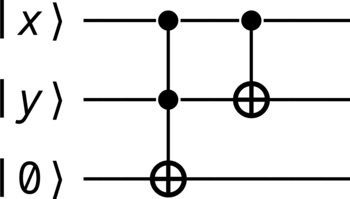
We consider here perhaps the simplest form of a quantum adder: a half adder (see Figure 16). In addition to producing a summation output value

(338)#\[s = x \oplus y,\]

a half adder also produces a carry output value

(339)#\[c^\prime = xy,\]

which represents the overflow of the summation. This is simply the value by which the modular sum of the inputs \(x\) and \(y\) is larger than the modulus \(\Dimension\). The form of a half adder presented here was first described by Feynman [6] in the context of quantum computing.

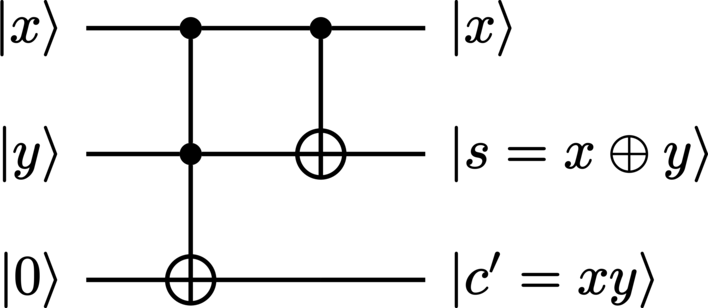
A quantum circuit diagram of a quantum half adder.

A truth table for this circuit in the context of qubits appears in Table 7.

Table 7 Truth table for a half adder.#
\(x\) (augend)	\(y\) (addend)	\(s\) (sum)	\(c^\prime\) (carry)
\(0\)	\(0\)	\(0\)	\(0\)
\(1\)	\(0\)	\(1\)	\(0\)
\(0\)	\(1\)	\(1\)	\(0\)
\(1\)	\(1\)	\(0\)	\(1\)

Implementation#

Listing 16 /text/examples/algorithms/adder_half.py#

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit

# Input
augend_state = VectorState(spec=[("a", [0]), ("b", [1])], label="x")
addend_state = VectorState(spec=[(1, [1])], label="y")
zero_state = VectorState(spec=[(1, [0])], label="0")

# Gates
CCN = Not(targets=[2], controls=[0, 1], num_systems=3)
CNI = Not(targets=[1], controls=[0], num_systems=3)

# Circuit
adder = QuantumCircuit(
    inputs=[augend_state, addend_state, zero_state], gates=[CCN, CNI]
)
adder.diagram()

# Output
sum_state = adder.state(label="s", traces=[0, 2])
carry_output_state = adder.state(label="c'", traces=[0, 1])

# Results
augend_state.print()
addend_state.print()
sum_state.print()
carry_output_state.print()

Output#

Diagram#

>>> adder.diagram()

States#

>>> augend_state.print()
|x⟩ = a|0⟩ + b|1⟩

>>> addend_state.print()
|y⟩ = |1⟩

>>> sum_state.print()
s = b*conjugate(b)|0⟩⟨0| + a*conjugate(a)|1⟩⟨1|

>>> carry_output_state.print()
c' = a*conjugate(a)|0⟩⟨0| + b*conjugate(b)|1⟩⟨1|

References

[1]

R. P. Feynman, “Quantum mechanical computers”, Foundations of Physics, 16(6):507–531, June 1986. https://doi.org/10.1007/BF01886518, doi:10.1007/BF01886518