Ripple-carry adder

Description

In this example, we use the single quantum adder circuit described in Full adder to construct a quantum ripple-carry adder. Given two (non-negative) integers \(x\) and \(y\) (encoded using qubits) as input, a ripple-carry adder computes the (encoded) arithmetic sum \(s\) of these integers, that is, \(s = x + y\). In this form, the two integers are known as summands, and are also specifically called augend (\(x\)) and addend (\(y\)) according to the order in which they appear in the addition operation.

In the case of a single adder, the magnitudes of the summands and their sum are confined to being within the dimensionality (e.g., binary) of their single-unit (e.g., bit) encoding. Integers larger than this limit therefore require multiple units of information to be encoded. For example, a non-negative integer \(z\) can be encoded with a number \(\Number\) of \(\Dimension\)-dimensional unit values provided \(z \leq \Dimension^\Number - 1\). Under this encoding, the integer can be represented using an ordered array (or set or string) of such values,

(342)\[z \equiv (z_{\Number - 1}, z_{\Number - 2}, \ldots, z_1, z_0) = (z_n)_{n = 0}^{\Number - 1}\]

which collectively reconstruct the (decimal) value of the integer with the unique decoding expansion

(343)\[\begin{split}\begin{aligned} z &= \sum_{n = 0}^{\Number - 1} z_n \Dimension^n \\ &= z_0\Dimension^0 + z_1\Dimension^1 + \ldots + z_{\Number - 2}\Dimension^{\Number - 2} + z_{\Number - 1}\Dimension^{\Number - 1}. \end{aligned}\end{split}\]

This is a type of unsigned integer encoding: all units of information are used to store the magnitude of the number, and there is no unit (e.g., a sign bit) reserved for storing the sign of the integer. It is perhaps the simplest integer encoding scheme possible, and so can be readily implemented in the context of quantum computing by utilizing the ability of quantum states to store information (both classical and quantum). This is typically realized using \(2\)-dimensional (binary) qubits (due to their simplicity), and so a collection of \(\Number\) such states allows for the encoding of (non-negative) integers up to \(2^\Number - 1\) via the scheme described in (342) and (343). The addition of any two such encoded integers, for example,

(344)\[\begin{split}\begin{aligned} \ket{x} &\equiv \bigotimes_{n = \Number - 1}^{0}\ket{x_n} = \ket{x_{\Number - 1},x_{\Number - 2},\ldots,x_1,x_0}, \\ \ket{y} &\equiv \bigotimes_{n = \Number - 1}^{0}\ket{y_n} = \ket{y_{\Number - 1},y_{\Number - 2},\ldots,y_1,y_0}, \end{aligned}\end{split}\]

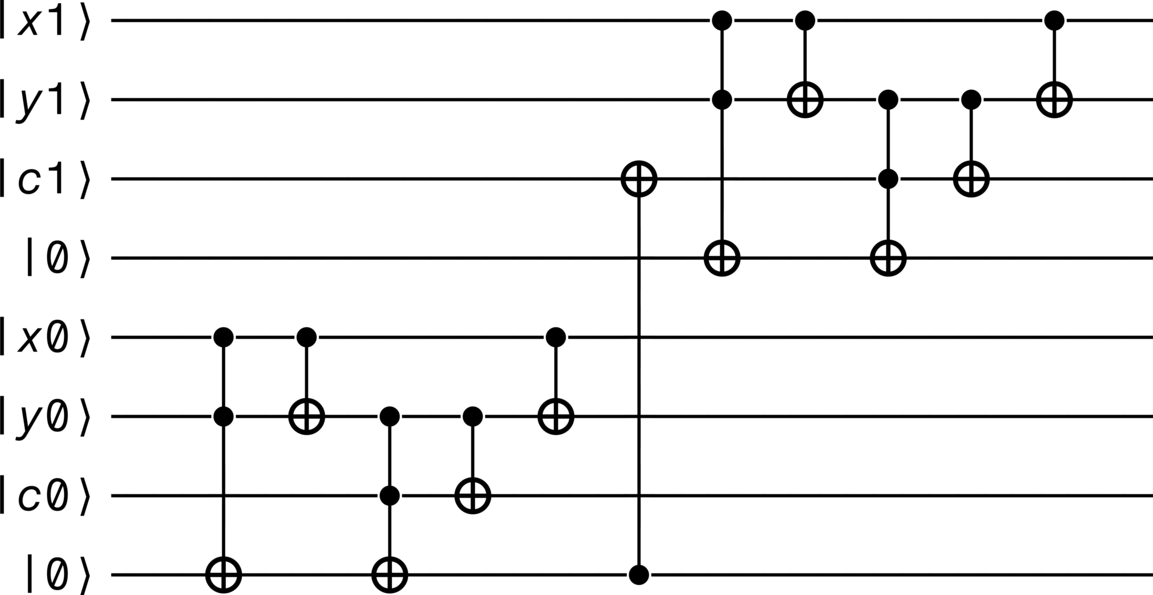
can then be accomplished by a succession of exactly \(\Number\) quantum ripple-carry adders. Each of these adders is applied to a different pair of subsystems in the encoded integers’ states—the first acts on the least significant qubit (\(n = 0\)), with the carry qubit from the previous adder being used as input to the next one. An example of this for a \(2\)-qubit encoding (\(\Number = 2\)) is depicted in Figure 18.

Figure 18 A \(2\)-qubit quantum ripple-carry adder. The CNOT operation between the FULL ADDER subcircuits transfers the value of the previous iteration’s carry output to the carry input of the next iteration.

From this circuit, the general output values of the summation qubits can be computed to be

(345)\[\begin{split}s_i = \begin{cases} x_0 \oplus y_0 \oplus c_0, & \text{if } i = 0; \\ x_i \oplus y_i \oplus c_i \oplus c^\prime_{i - 1}, & \text{if } i > 0; \\ \end{cases}\end{split}\]

while the carry values are

(346)\[\begin{split}c^\prime_i = \begin{cases} x_0 y_0 \oplus y_0 c_0 \oplus x_0 c_0, & \text{if } i = 0; \\ x_i y_i \oplus (x_i \oplus y_i)(c_i \oplus c^\prime_{i-1}), & \text{if } i > 0. \\ \end{cases}\end{split}\]

With these, the corresponding states

(347)\[\begin{split}\begin{aligned} \ket{s} &\equiv \bigotimes_{n = \Number - 1}^{0}\ket{s_n}, \\ \ket{c^\prime} &\equiv \bigotimes_{n = \Number - 1}^{0}\ket{c^\prime_n}, \end{aligned}\end{split}\]

can be decoded, using (343), to be

(348)\[\begin{split}\begin{aligned} s &= \sum_{n = 0}^{\Number - 1} s_n \Dimension^n, \\ c^\prime &= \sum_{n = 0}^{\Number - 1} c^\prime_n \Dimension^n. \end{aligned}\end{split}\]

Implementation

Due to performance constraints, this example sums two 2-bit integers. Increasing the encoding_depth greatly increases the calculation time as a result of having to perform operations on larger matrices. The decimal augend_integer and addend_integer variables can be freely changed, provided their summation is within the encodable range.

Listing 18 /text/examples/algorithms/adder_ripple.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.utilities.helpers import flatten_list
from qhronology.mechanics.matrices import encode, decode, decode_fast

import sympy as sp

import time

initial_time = time.time()

augend_integer = 1
addend_integer = 1
encoding_depth = 2

# Input
augend_state = VectorState(
    spec=encode(integer=augend_integer, num_systems=encoding_depth), label="x"
)
addend_state = VectorState(
    spec=encode(integer=addend_integer, num_systems=encoding_depth), label="y"
)

augend_states = []
addend_states = []
carry_states = []
zero_states = []
for i in range(0, encoding_depth):
    target_bit = i
    complement_bits = [n for n in range(0, encoding_depth) if n != target_bit]

    augend_state.partial_trace(complement_bits)
    addend_state.partial_trace(complement_bits)

    augend_bit = decode(augend_state.output())
    addend_bit = decode(addend_state.output())

    augend_bit_state = VectorState(
        spec=encode(augend_bit, 1),
        label=augend_state.label + str(encoding_depth - 1 - i),
    )
    addend_bit_state = VectorState(
        spec=encode(addend_bit, 1),
        label=addend_state.label + str(encoding_depth - 1 - i),
    )
    carry_state = VectorState(
        spec=encode(0, 1), label="c" + str(encoding_depth - 1 - i)
    )
    zero_state = VectorState(spec=encode(0, 1), label="0")

    augend_states.append(augend_bit_state)
    addend_states.append(addend_bit_state)
    carry_states.append(carry_state)
    zero_states.append(zero_state)

    augend_state.reset()
    addend_state.reset()

input_spec = flatten_list(
    [
        [augend_states[i], addend_states[i], carry_states[i], zero_states[i]]
        for i in range(0, encoding_depth)
    ]
)

# Gates
gates = []
for i in range(0, encoding_depth):
    system_shift = 4 * (encoding_depth - 1 - i)

    CCIN = Not(
        targets=[system_shift + 3],
        controls=[system_shift + 0, system_shift + 1],
        num_systems=4 * encoding_depth,
    )
    CNII = Not(
        targets=[system_shift + 1],
        controls=[system_shift + 0],
        num_systems=4 * encoding_depth,
    )
    ICCN = Not(
        targets=[system_shift + 3],
        controls=[system_shift + 1, system_shift + 2],
        num_systems=4 * encoding_depth,
    )
    ICNI = Not(
        targets=[system_shift + 2],
        controls=[system_shift + 1],
        num_systems=4 * encoding_depth,
    )

    adder_single = [CCIN, CNII, ICCN, ICNI, CNII]
    gates.append(adder_single)

    if i != max(range(0, encoding_depth)):
        CNOT = Not(
            targets=[system_shift - 2],
            controls=[system_shift + 3],
            num_systems=4 * encoding_depth,
        )
        adder_single.append(CNOT)

gates = flatten_list(gates)

# Circuit
adder = QuantumCircuit(inputs=input_spec, gates=gates)
adder.diagram()

# Output
sum_registers = [2 + i * 4 for i in range(0, encoding_depth)]
not_sum_registers = [i for i in range(0, 4 * encoding_depth) if i not in sum_registers]
sum_state = adder.state(label="s", traces=not_sum_registers)
sum_integer = decode_fast(sum_state.output())
sum_state = VectorState(spec=encode(sum_integer), label="s")

# Results
augend_state.print()
addend_state.print()
sum_state.print()

final_time = time.time()
computation = f"Computation: {augend_integer} + {addend_integer} = {sum_integer}"
duration = f"Duration: {sp.N(final_time - initial_time,8).round(3)} seconds"
print(computation)
print(duration)

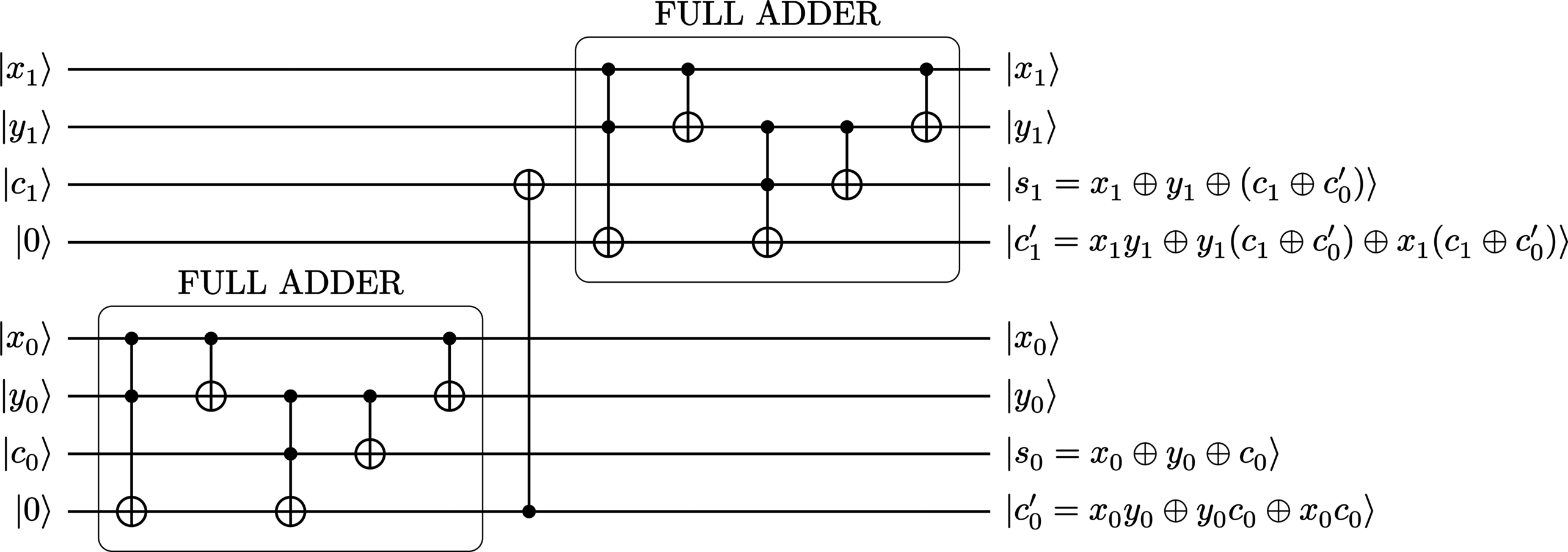
Output

Diagram

>>> adder.diagram()

States

>>> augend_state.print()
|x⟩ = |0,1⟩

>>> addend_state.print()
|y⟩ = |0,1⟩

>>> sum_state.print()
|s⟩ = |1,0⟩

Results

>>> print(computation)
Computation: 1 + 1 = 2

>>> print(duration)
Duration: 14.913 seconds

This is of course extremely slow, mainly due to the computations involving relatively large matrices in the underlying calculation. Optimization of Qhronology’s linear algebra algorithms, particularly the partial trace implementation, should improve both efficiency and speed.