Generation of a generalized GHZ state

Description

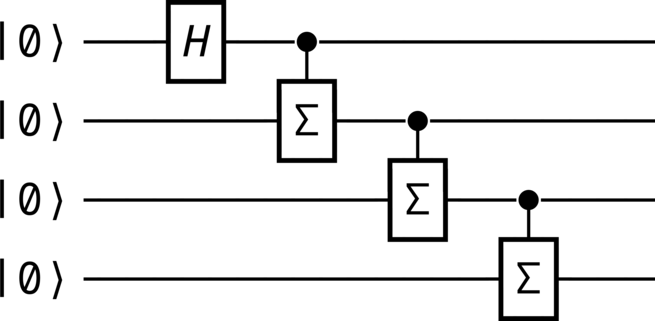
The circuit in Figure 10 illustrates an algorithm for the generation of an entangled \(\Number\)-qudit state,

(327)\[\begin{split}\begin{aligned} \ket{\mathrm{GHZ}} &= \frac{1}{\sqrt{\Dimension}} \sum_{k=0}^{\Dimension - 1} \bigotimes_{n=1}^{\Number} \ket{k} \\ &= \frac{1}{\sqrt{\Dimension}} \sum_{k=0}^{\Dimension - 1} \ket{k}^{\otimes \Number} \\ &= \frac{1}{\sqrt{\Dimension}} \sum_{k=0}^{\Dimension - 1} \ket{k} \otimes \ldots \otimes \ket{k}, \end{aligned}\end{split}\]

from primitive \(\ket{0}\) states. This is also known as the generalized GHZ state (see Generation of a GHZ state).

Figure 10 Generation of a generalized GHZ state.

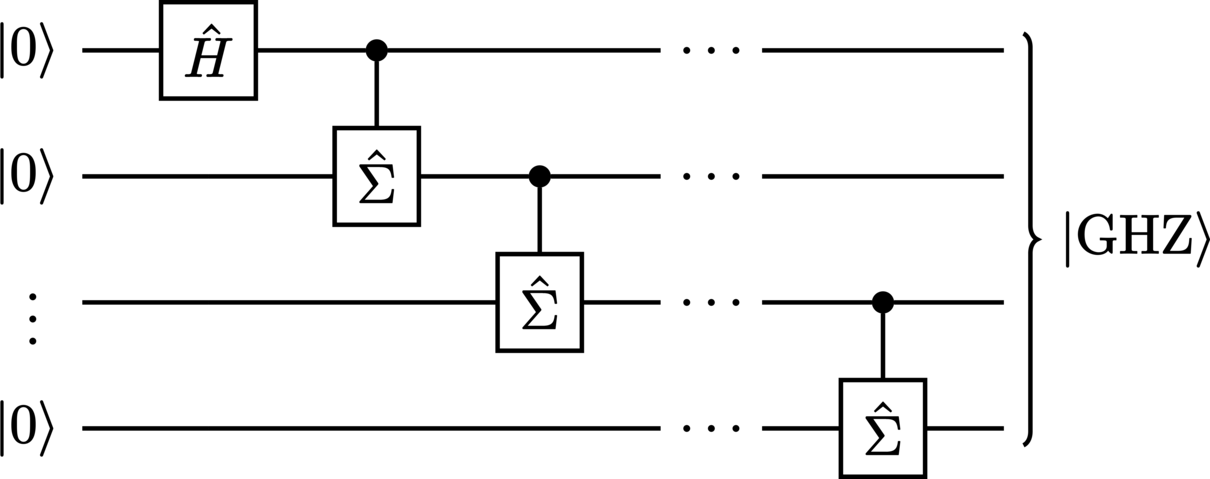
The complete unitary transformation described by this circuit is the product

(328)\[\begin{split}\begin{aligned} \Unitary &= \Control^{\Number - 2} \SUM^{\Number - 1} \cdot \ldots \cdot \Control^1 \SUM^2 \cdot \Control^0 \SUM^1 \cdot \Hadamard^0 \\ &= \Biggl(\prod_{n = \Number - 1}^{1} \Control^{n - 1} \SUM^{n} \Biggr) \Hadamard^0. \end{aligned}\end{split}\]

Implementation

Listing 10 /text/examples/algorithms/generation_ghz_general.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Hadamard, Summation
from qhronology.quantum.circuits import QuantumCircuit

num_systems = 4
dim = 4

# Input
zero_state = VectorState(spec=[(1, [0])], label="0", dim=dim)
input_states = [zero_state for i in range(0, num_systems)]

# Gates
HII = Hadamard(targets=[0], num_systems=num_systems, dim=dim)
CNOTs = [
    Summation(targets=[i + 1], controls=[i], num_systems=num_systems, dim=dim)
    for i in range(0, num_systems - 1)
]

gates = [HII] + CNOTs

# Circuit
generator = QuantumCircuit(inputs=input_states, gates=gates)
generator.diagram()

# Output
ghz_state = generator.state(label="GHZ")

# Results
ghz_state.print()

Output

Diagram

>>> generator.diagram()

State

>>> ghz_state.print()
|GHZ⟩ = 1/2|0,0,0,0⟩ + 1/2|1,1,1,1⟩ + 1/2|2,2,2,2⟩ + 1/2|3,3,3,3⟩