iSWAP (imaginary-SWAP)

Description

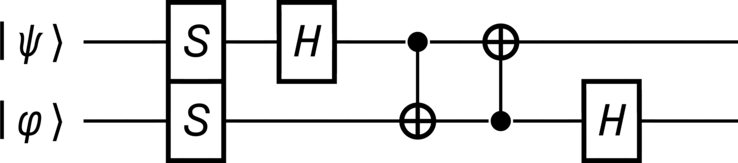
An iSWAP (imaginary-SWAP) gate is a simply a SWAP gate in which any pair of states that are exchanged are also multiplied by a phase factor of \(\e^{\tfrac{\eye\pi}{2}} = \eye\) (the imaginary unit). It can be constructed from \(\op{S}\) (\(\op{Z}^{\tfrac{1}{2}}\)) gates, \(\Hadamard\) (Hadamard) gates, and CNOT gates, as depicted in Figure 25.

Figure 25 One possible construction of the iSWAP gate.

Implementation

Listing 24 /text/examples/algorithms/iswap.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Pauli, Hadamard, Not, GateStack
from qhronology.quantum.circuits import QuantumCircuit

# Input
psi = VectorState(
    spec=[("a", [0]), ("b", [1])],
    symbols={"a": {"complex": True}, "b": {"complex": True}},
    conditions=[("a*conjugate(a) + b*conjugate(b)", "1")],
    label="ψ",
)
phi = VectorState(
    spec=[("c", [0]), ("d", [1])],
    symbols={"c": {"complex": True}, "d": {"complex": True}},
    conditions=[("c*conjugate(c) + d*conjugate(d)", "1")],
    label="φ",
)

# Gates
S = Pauli(index=3, exponent=1 / 2, label="S")
SS = GateStack(S, S)
HI = Hadamard(targets=[0], num_systems=2)
CN = Not(targets=[1], controls=[0])
NC = Not(targets=[0], controls=[1])
IH = Hadamard(targets=[1], num_systems=2)

# Circuit
iswap = QuantumCircuit(inputs=[psi, phi], gates=[SS, HI, CN, NC, IH])
iswap.diagram()

# Output
input_state = QuantumCircuit(inputs=[psi, phi]).state(label="ψ,φ")
output_state = iswap.state(label="(ψ,φ)'")
output_state.simplify()

# Results
print(repr(iswap.gate(simplify=True)))
input_state.print()
output_state.print()

Output

Diagram

>>> iswap.diagram()

Gate

>>> print(repr(iswap.gate()))
Matrix([
[1, 0, 0, 0],
[0, 0, I, 0],
[0, I, 0, 0],
[0, 0, 0, 1]])

States

>>> input_state.print()
|ψ,φ⟩ = a*c|0,0⟩ + a*d|0,1⟩ + b*c|1,0⟩ + b*d|1,1⟩

>>> output_state.print()
|(ψ,φ)'⟩ = a*c|0,0⟩ + I*b*c|0,1⟩ + I*a*d|1,0⟩ + b*d|1,1⟩