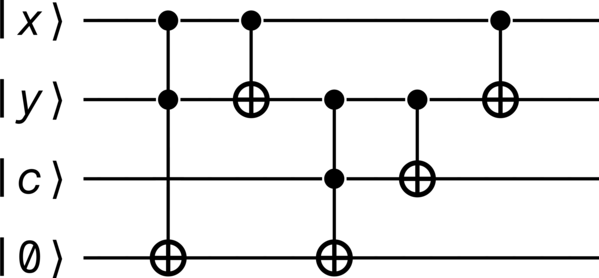
Full adder

Description

A full adder is simply an adder with three (non-zero) inputs, as opposed to the two of a half adder. With the first and second of these inputs being the ordinary pair of values to be summed (e.g., \(x\) and \(y\)), a full adder’s third input is used to modify the addition operation. This enables the circuit to take into account the carry output value \(c\) of a previous iteration, yielding the summation output

(340)\[s = x \oplus y \oplus c,\]

and the carry output

(341)\[c^\prime = xy \oplus yc \oplus xc.\]

Importantly, this means that full adders can be used in succession as a way to sum multi-qubit-encoded numbers. Like the half adder, the full adder (as it is presented here in Figure 17) was first studied by Feynman [6].

Figure 17 A quantum full adder.

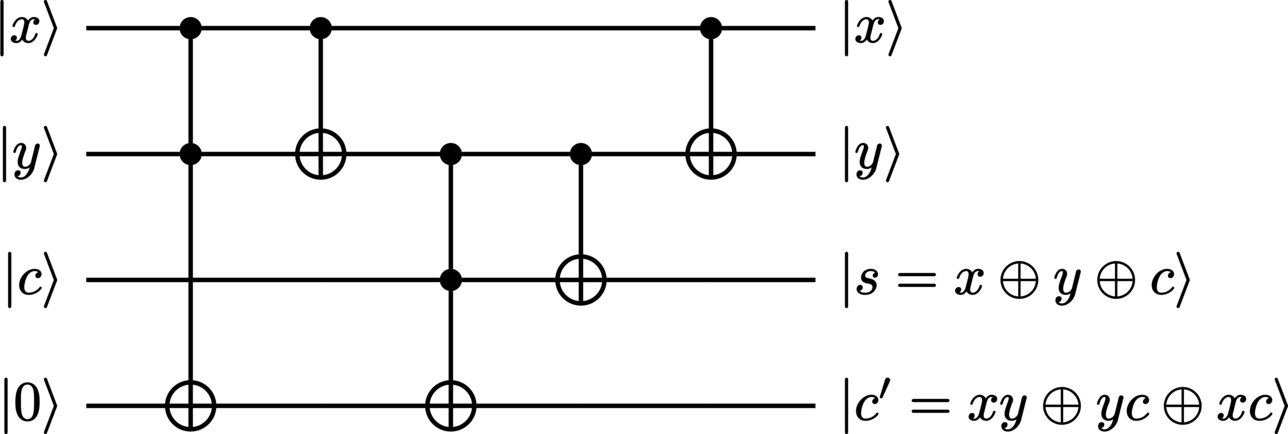
A truth table for this circuit in the context of qubits appears in Table 8.

Table 8 Truth table for the full adder.

\(x\) (augend)	\(y\) (addend)	\(c\) (carry input)	\(s\) (sum)	\(c^\prime\) (carry output)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)
\(1\)	\(0\)	\(0\)	\(1\)	\(0\)
\(0\)	\(1\)	\(0\)	\(1\)	\(0\)
\(1\)	\(1\)	\(0\)	\(0\)	\(1\)
\(0\)	\(0\)	\(1\)	\(1\)	\(0\)
\(1\)	\(0\)	\(1\)	\(0\)	\(1\)
\(0\)	\(1\)	\(1\)	\(0\)	\(1\)
\(1\)	\(1\)	\(1\)	\(1\)	\(1\)

Implementation

Listing 17 /text/examples/algorithms/adder_full.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit

augend_integers = [0, 1]
addend_integers = 1

# Input
augend_state = VectorState(
    spec=[("a", [0]), ("b", [1])],
    conditions=[("a*conjugate(a) + b*conjugate(b)", 1)],
    label="x",
)
addend_state = VectorState(spec=[(1, [1])], label="y")
carry_input_state = VectorState(spec=[(1, [1])], label="c")
zero_state = VectorState(spec=[(1, [0])], label="0")

# Gates
CCIN = Not(targets=[3], controls=[0, 1], num_systems=4)
CNII = Not(targets=[1], controls=[0], num_systems=4)
ICCN = Not(targets=[3], controls=[1, 2], num_systems=4)
ICNI = Not(targets=[2], controls=[1], num_systems=4)

# Circuit
adder = QuantumCircuit(
    inputs=[augend_state, addend_state, carry_input_state, zero_state],
    gates=[CCIN, CNII, ICCN, ICNI, CNII],
)
adder.diagram()

# Output
sum_state = adder.state(label="s", traces=[0, 1, 3])
carry_output_state = adder.state(label="c'", traces=[0, 1, 2])

# Results
augend_state.print()
addend_state.print()
carry_input_state.print()
sum_state.print()
carry_output_state.print()

Output

Diagram

>>> adder.diagram()

States

>>> augend_state.print()
|x⟩ = a|0⟩ + b|1⟩

>>> addend_state.print()
|y⟩ = |1⟩

>>> carry_input_state.print()
|c⟩ = |1⟩

>>> sum_state.print()
s = a*conjugate(a)|0⟩⟨0| + b*conjugate(b)|1⟩⟨1|

>>> carry_output_state.print()
c' = |1⟩⟨1|

References

[1]

R. P. Feynman, “Quantum mechanical computers”, Foundations of Physics, 16(6):507–531, June 1986. https://doi.org/10.1007/BF01886518, doi:10.1007/BF01886518