Quantum teleportation#
Description#
Quantum teleportation [1] is a significant technique of quantum theory in which the transfer of quantum information between two parties (that may be spatially separated) is achieved. Importantly, this does not involve the movement of physical entities, but concerns rather the transfer of the (quantum) statistics of a physical system (manifesting as a quantum state) to another. This is facilitated by a pair of entangled particles, the statistical correlations of which provide the actual mechanism of teleportation.
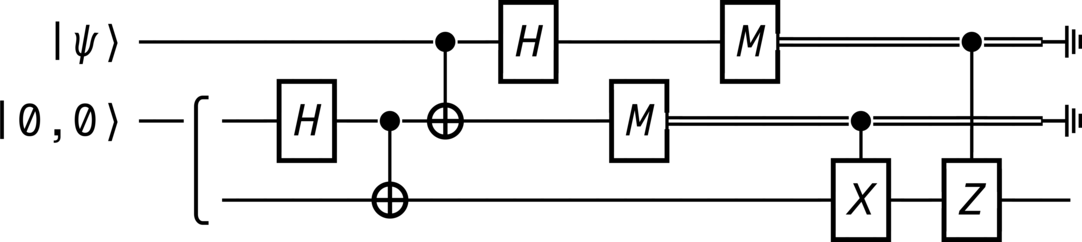
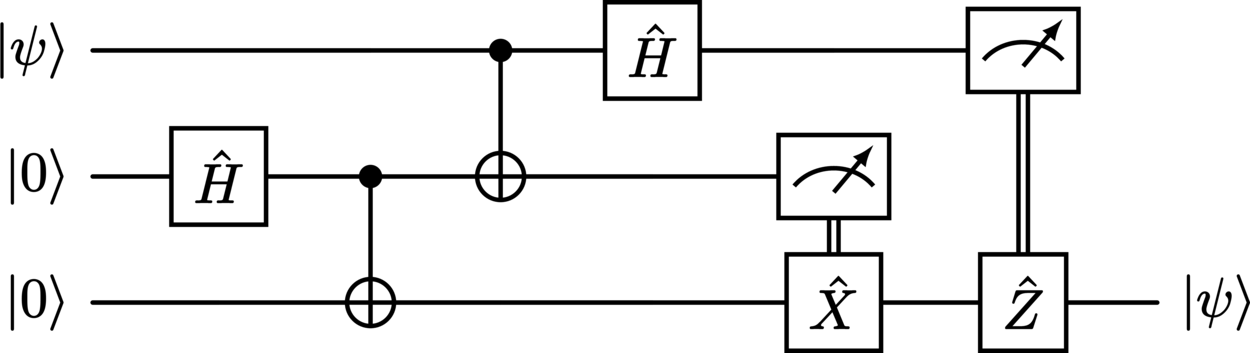
Note that in the process of teleporting the state, the original is destroyed, and so the no-cloning theorem remains unviolated. Additionally, because classical information needs to be sent between the two parties, the teleportation cannot occur faster than the speed of light, meaning that the law of relativity is satisfied. This example (Figure 23) implements the canonical version of the algorithm.
Implementation#
from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Hadamard, Not, Measurement, Pauli
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.mechanics.matrices import ket
# Input
teleporting_state = VectorState(
spec=[["a", "b"]],
symbols={"a": {"complex": True}, "b": {"complex": True}},
conditions=[("a*conjugate(a) + b*conjugate(b)", "1")],
label="ψ",
)
zero_state = VectorState(spec=[(1, [0, 0])], label="0,0")
# Gates
IHI = Hadamard(targets=[1], num_systems=3)
ICN = Not(targets=[2], controls=[1], num_systems=3)
CNI = Not(targets=[1], controls=[0], num_systems=3)
HII = Hadamard(targets=[0], num_systems=3)
IMI = Measurement(
operators=[ket(0), ket(1)], observable=False, targets=[1], num_systems=3
)
MII = Measurement(
operators=[ket(0), ket(1)], observable=False, targets=[0], num_systems=3
)
ICX = Pauli(index=1, targets=[2], controls=[1], num_systems=3)
CIZ = Pauli(index=3, targets=[2], controls=[0], num_systems=3)
# Circuit
teleporter = QuantumCircuit(
inputs=[teleporting_state, zero_state],
gates=[IHI, ICN, CNI, HII, IMI, MII, ICX, CIZ],
traces=[0, 1],
)
teleporter.diagram(force_separation=True)
# Output
teleported_state = teleporter.state(norm=1, label="ρ")
# Results
teleporting_state.print()
teleported_state.print()
print(teleporting_state.distance(teleported_state))
print(teleporting_state.fidelity(teleported_state))
Output#
Diagram#
>>> teleporter.diagram(force_separation=True)
States#
>>> teleporting_state.print()
|ψ⟩ = a|0⟩ + b|1⟩
>>> teleported_state.print()
ρ = a*conjugate(a)|0⟩⟨0| + a*conjugate(b)|0⟩⟨1| + b*conjugate(a)|1⟩⟨0| + b*conjugate(b)|1⟩⟨1|
Results#
>>> teleporting_state.distance(teleported_state)
0
>>> teleporting_state.fidelity(teleported_state)
1
References
C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. K. Wootters, “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels”, Physical Review Letters, 70(13):1895–1899, 1993. https://link.aps.org/doi/10.1103/PhysRevLett.70.1895, doi:10.1103/PhysRevLett.70.1895