Toffoli decomposition

Description

An important research subfield of quantum computing involves the (de)construction of complex gates using sets of more primitive gates. This is termed decomposition, and mostly concerns the task of finding the (most) minimal gate set (i.e., most restricted) for any given gate. It is an interesting problem as primitive gates are in fact usually the only gates which can be directly implemented in many physical quantum computers. Consequently, finding compositions of such primitives that correctly reconstruct more complex gates is necessary in the pursuit of executing more advanced algorithms. Balancing the depth of the circuit (i.e., the longest path along its wires from input to output) with minimizing the size of the gate set also forms an avenue of research, as a circuit’s depth generally correlates with its execution time (discounting any execution time differences between the various types of gates).

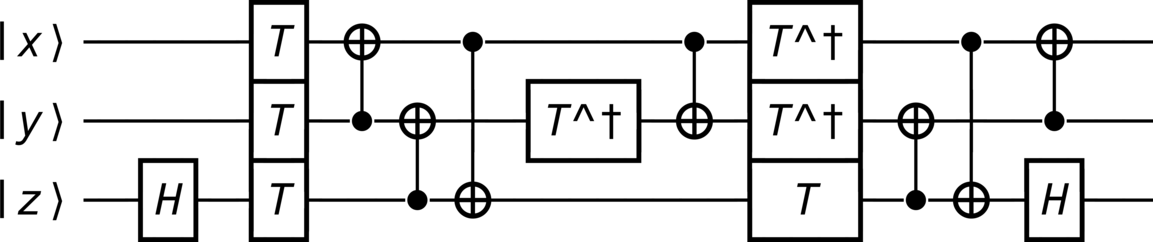
The Toffoli gate, also known as the CCNOT gate (see CCNOT (controlled-controlled-NOT)), is one such gate that can be decomposed into more primitive gates. As it is an entangling gate, the Toffoli’s gate set must include more than just the single-qubit rotation gates (such as the \(\op{T}\) gate), as all such gates describe non-entangling operations. Thus, one such set of gates consists of the Hadamard gate \(\Hadamard\) and the CNOT gate, in addition to the \(\op{T}\) gate (fourth root of \(\op{Z}\), i.e., \(\op{Z}^{\tfrac{1}{4}}\)). Using this restricted set, one possible decomposition of the Toffoli gate appears in Figure 15. Note that the conjugate transpose of any gate in the set, e.g., \(\op{T}^\dagger\), is considered to also be in the set.

Figure 15 One possible decomposition of the Toffoli gate.

Implementation

Listing 15 /text/examples/algorithms/toffoli.py

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Hadamard, Phase, Not, GateInterleave
from qhronology.quantum.circuits import QuantumCircuit

import sympy as sp

# Input
first_state = VectorState(
    spec=[("a", [0]), ("b", [1])],
    symbols={"a": {"complex": True}, "b": {"complex": True}},
    conditions=[("a*conjugate(a) + b*conjugate(b)", "1")],
    label="x",
)
second_state = VectorState(
    spec=[("c", [0]), ("d", [1])],
    symbols={"c": {"complex": True}, "d": {"complex": True}},
    conditions=[("c*conjugate(c) + d*conjugate(d)", "1")],
    label="y",
)
third_state = VectorState(
    spec=[("u", [0]), ("v", [1])],
    symbols={"u": {"complex": True}, "v": {"complex": True}},
    conditions=[("u*conjugate(u) + v*conjugate(v)", "1")],
    label="z",
)

# Gates
IIH = Hadamard(targets=[2], num_systems=3)
TII = Phase(exponent=sp.Rational(1, 4), targets=[0], num_systems=3, label="T")
ITI = Phase(exponent=sp.Rational(1, 4), targets=[1], num_systems=3, label="T")
IIT = Phase(exponent=sp.Rational(1, 4), targets=[2], num_systems=3, label="T")
TTT = GateInterleave(TII, ITI, IIT)
NCI = Not(targets=[0], controls=[1], num_systems=3)
INC = Not(targets=[1], controls=[2], num_systems=3)
CIN = Not(targets=[2], controls=[0], num_systems=3)
CNI = Not(targets=[1], controls=[0], num_systems=3)
ItI = Phase(
    exponent=sp.Rational(1, 4), conjugate=True, targets=[1], num_systems=3, label="T^†"
)
tII = Phase(
    exponent=sp.Rational(1, 4), conjugate=True, targets=[0], num_systems=3, label="T^†"
)
ttT = GateInterleave(tII, ItI, IIT)
NCH = GateInterleave(NCI, IIH)

# Circuit
circuit = QuantumCircuit(
    inputs=[first_state, second_state, third_state],
    gates=[IIH, TTT, NCI, INC, CIN, ItI, CNI, ttT, INC, CIN, NCH],
)
circuit.diagram(force_separation=True)

# Output
output_state = circuit.state(label="x, y, z ⊕ xy")

# Results
first_state.print()
second_state.print()
third_state.print()
output_state.print()

Output

Diagram

>>> circuit.diagram(force_separation = True)

States

>>> first_state.print()
|x⟩ = a|0⟩ + b|1⟩

>>> second_state.print()
|y⟩ = c|0⟩ + d|1⟩

>>> third_state.print()
|z⟩ = u|0⟩ + v|1⟩

>>> output_state.print()
|x, y, z ⊕ xy⟩ = a*c*u|0,0,0⟩ + a*c*v|0,0,1⟩ + a*d*u|0,1,0⟩ + a*d*v|0,1,1⟩ + b*c*u|1,0,0⟩ + b*c*v|1,0,1⟩ + b*d*v|1,1,0⟩ + b*d*u|1,1,1⟩