CNOT (controlled-NOT)#

Description#

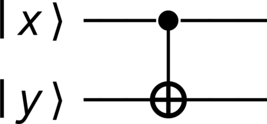
A CNOT (controlled-NOT) gate is a useful gate for performing a (qu)bit-wise sum of the state values of two quantum systems. For instance, given the states \(\ket{x}\) and \(\ket{y}\) in a \(\Dimension\)-dimensional basis \(\{\ket{n}\}_{n=0}^{\Dimension - 1}\), a CNOT operation has the action

(332)#\[\ket{x} \otimes \ket{y} \rightarrow \ket{x} \otimes \ket{x \oplus y}.\]

A circuit diagram of a CNOT gate appears in Figure 13.

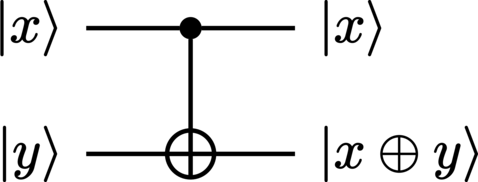
A quantum circuit diagram of a CNOT (controlled-NOT) gate.

As the input states are both vectors, the application of the CNOT gate

(333)#\[\begin{split}\begin{aligned} \Unitary &= \Control^0 \NOT^1 \\ &= \Identity \otimes \Identity + {\ket{1}\bra{1}} \otimes (\Pauli_{x} - \Identity), \end{aligned}\end{split}\]

on the bipartite input \(\ket{x} \otimes \ket{y}\) simply produces a vector state:

(334)#\[\begin{split}\begin{aligned} \MapGeneral_{\Unitary} \bigl[\ket{x} \otimes \ket{y}\bigr] &= \Control^0 \NOT^1 \ket{x} \otimes \ket{y} \\ % &= \sum\limits_{a,b=0}^{1} {\ket{a}\braket{a}{x}} \otimes {\ket{b \oplus a}\braket{b}{y}}, \\ &= \ket{x} \otimes \ket{x \oplus y} \end{aligned}\end{split}\]

Observe how the value of the second system is now the sum of the inputs values (modulo the dimensionality), so if we simply discard (trace over) the first system, we obtain our desired result. A truth table for qubits appears in Table 5.

Table 5 Truth table of the CNOT gate.#
\(x\)	\(y\)	\(x \oplus y\)
\(0\)	\(0\)	\(0\)
\(1\)	\(0\)	\(1\)
\(0\)	\(1\)	\(1\)
\(1\)	\(1\)	\(0\)

Implementation#

Listing 13 /text/examples/algorithms/cnot.py#

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit

# Input
first_state = VectorState(
    spec=[("a", [0]), ("b", [1])],
    symbols={"a": {"complex": True}, "b": {"complex": True}},
    conditions=[("a*conjugate(a) + b*conjugate(b)", "1")],
    label="x",
)
second_state = VectorState(
    spec=[("c", [0]), ("d", [1])],
    symbols={"c": {"complex": True}, "d": {"complex": True}},
    conditions=[("c*conjugate(c) + d*conjugate(d)", "1")],
    label="y",
)

# Gate
CN = Not(targets=[1], controls=[0], num_systems=2)

# Circuit
circuit = QuantumCircuit(inputs=[first_state, second_state], gates=[CN])
circuit.diagram()

# Output
output_state = circuit.state(label="x, x ⊕ y")

# Results
first_state.print()
second_state.print()
output_state.print()

Output#

Diagram#

>>> circuit.diagram()

States#

>>> first_state.print()
|x⟩ = a|0⟩ + b|1⟩

>>> second_state.print()
|y⟩ = c|0⟩ + d|1⟩

>>> output_state.print()
|x, x ⊕ y⟩ = a*c|0,0⟩ + a*d|0,1⟩ + b*d|1,0⟩ + b*c|1,1⟩