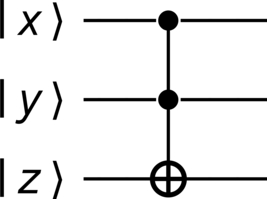
CCNOT (controlled-controlled-NOT)#

Description#

A CCNOT (controlled-controlled-NOT) gate, also known as a Toffoli gate, is a simple extension to a CNOT gate (see CNOT (controlled-NOT)). It is useful as a method of multiplying the values of two qubits (e.g., \(\ket{x}\) and \(\ket{y}\)), and imprinting this result onto a third qubit (e.g., \(\ket{z}\)), e.g.,

(335)#\[\ket{x} \otimes \ket{y} \otimes \ket{z} \rightarrow \ket{x} \otimes \ket{y} \otimes \ket{z \oplus xy}.\]

Figure 14 visualizes this operation.

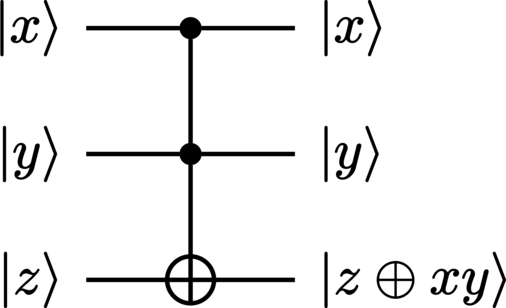
A quantum circuit diagram of a CCNOT (controlled-controlled-NOT) gate.

As the input states are both vectors, the action of the (linear) CCNOT gate, described by the unitary

(336)#\[\begin{split}\begin{aligned} \Unitary &= \Control^{0,1} \NOT^2 \\ &= \Identity \otimes \Identity \otimes \Identity + {\ket{1}\bra{1}} \otimes {\ket{1}\bra{1}} \otimes (\Pauli_{x} - \Identity), \end{aligned}\end{split}\]

on the tripartite input \(\ket{x} \otimes \ket{y} \otimes \ket{z}\) yields a vector state:

(337)#\[\begin{split}\begin{aligned} \MapGeneral_{\Unitary} \bigl[\ket{x} \otimes \ket{y} \oplus \ket{z}\bigr] &= \Control^{0,1} \NOT^2 \ket{x} \otimes \ket{y} \oplus \ket{z} \\ &= \ket{x} \otimes \ket{y} \otimes \ket{z \oplus x y} \end{aligned}\end{split}\]

Table 6 is a truth table for this operation in the context of qubits.

Table 6 Truth table of the CCNOT gate.#
\(x\)	\(y\)	\(z\)	\(z \oplus x y\)
\(0\)	\(0\)	\(0\)	\(0\)
\(1\)	\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(0\)	\(0\)
\(1\)	\(1\)	\(0\)	\(1\)
\(0\)	\(0\)	\(1\)	\(1\)
\(1\)	\(0\)	\(1\)	\(1\)
\(0\)	\(1\)	\(1\)	\(1\)
\(1\)	\(1\)	\(1\)	\(0\)

Implementation#

Listing 14 /text/examples/algorithms/ccnot.py#

from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit

# Input
first_state = VectorState(
    spec=[("a", [0]), ("b", [1])],
    symbols={"a": {"complex": True}, "b": {"complex": True}},
    conditions=[("a*conjugate(a) + b*conjugate(b)", "1")],
    label="x",
)
second_state = VectorState(
    spec=[("c", [0]), ("d", [1])],
    symbols={"c": {"complex": True}, "d": {"complex": True}},
    conditions=[("c*conjugate(c) + d*conjugate(d)", "1")],
    label="y",
)
third_state = VectorState(
    spec=[("u", [0]), ("v", [1])],
    symbols={"u": {"complex": True}, "v": {"complex": True}},
    conditions=[("u*conjugate(u) + v*conjugate(v)", "1")],
    label="z",
)

# Gate
CCN = Not(targets=[2], controls=[0, 1], num_systems=3)

# Circuit
circuit = QuantumCircuit(inputs=[first_state, second_state, third_state], gates=[CCN])
circuit.diagram()

# Output
output_state = circuit.state(label="x, y, z ⊕ xy")

# Results
first_state.print()
second_state.print()
third_state.print()
output_state.print()

Output#

Diagram#

>>> circuit.diagram()

States#

>>> first_state.print()
|x⟩ = a|0⟩ + b|1⟩

>>> second_state.print()
|y⟩ = c|0⟩ + d|1⟩

>>> third_state.print()
|z⟩ = u|0⟩ + v|1⟩

>>> output_state.print()
|x, y, z ⊕ xy⟩ = a*c*u|0,0,0⟩ + a*c*v|0,0,1⟩ + a*d*u|0,1,0⟩ + a*d*v|0,1,1⟩ + b*c*u|1,0,0⟩ + b*c*v|1,0,1⟩ + b*d*v|1,1,0⟩ + b*d*u|1,1,1⟩