Carry-lookahead adder#

Description#

A quantum carry-lookahead adder, proposed by Vedral et al. [1], is another style of multi-qubit adder and appears in Figure 20. It consists of two phases: in the first, the carry qubits are computed, while in the second, the sums (taking into account the value of the carry qubits) are computed (in addition to the carry qubits being reverted back to their original values). Note that in this implementation, the order of the qubits in the encoding is reversed, such that the least-significant qubits are at the top while the most-significant qubits are at the bottom.

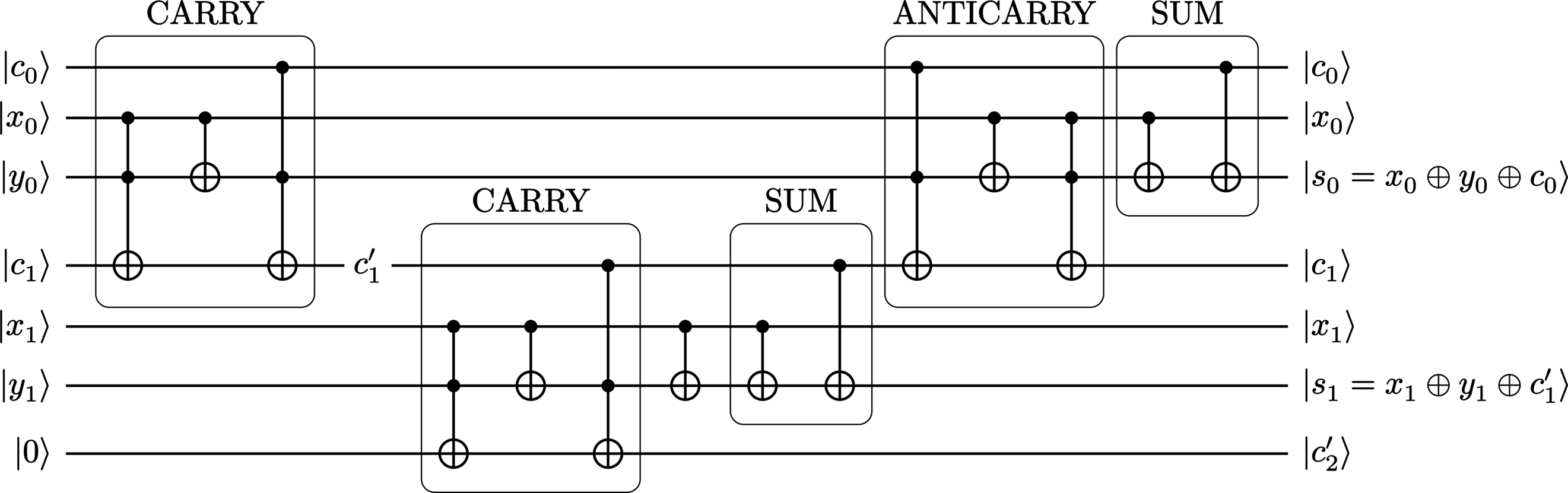
A quantum circuit diagram of a quantum carry-lookahead adder.
A quantum circuit diagram of a quantum carry-lookahead adder.

The values of the summation qubits can be determined to be

(349)#\[\begin{split}s_i = \begin{cases} x_0 \oplus y_0 \oplus c_0, & \text{if } i = 0; \\ x_i \oplus y_i \oplus c^\prime_i, & \text{if } i > 0. \\ \end{cases}\end{split}\]

This version of an adder resets all output carry qubits to their original input values. The intermediary carry values however are

(350)#\[\begin{split}c^\prime_i = \begin{cases} c_1 \oplus x_0 y_0 \oplus c_0 (x_0 \oplus y_0), & \text{if } i = 1; \\ c_i \oplus x_{i - 1} y_{i - 1} \oplus c^\prime_{i - 1} (x_{i - 1} \oplus y_{i - 1}), & \text{if } i > 1. \\ \end{cases}\end{split}\]

The last qubit is simply an overflow qubit and has the value

(351)#\[c^\prime_\Dimension = c_\Dimension \oplus x_{\Dimension - 1} y_{\Dimension - 1} \oplus c^\prime_{\Dimension - 1} (x_{\Dimension - 1} \oplus y_{\Dimension - 1}).\]

It is non-zero when the sum of the most-significant qubits (plus carry) “wraps around” (due to the modular arithmetic), and so represents the case where the total resulting sum is too big to be encoded with just \(\Dimension\) qubits, a situation known as integer overflow. If the value of this qubit is not required, then the circuit can be simplified by removing the last CARRY, the lone CNOT, and the qubit itself.

Implementation#

In this implementation, the dimensionality of the input state can be decreased by removing the overflow qubit (via overflow_qubit = False), thereby reducing the execution time of the algorithm.

Listing 20 /text/examples/algorithms/adder_lookahead.py#
from qhronology.quantum.states import VectorState
from qhronology.quantum.gates import Not
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.utilities.helpers import flatten_list
from qhronology.mechanics.matrices import encode, decode

import sympy as sp

import time

initial_time = time.time()

augend_integer = 1
addend_integer = 1
encoding_depth = 2
overflow_qubit = True

# Input
augend_state = VectorState(
    spec=encode(integer=augend_integer, num_systems=encoding_depth, reverse=True),
    label="x",
)
addend_state = VectorState(
    spec=encode(integer=addend_integer, num_systems=encoding_depth, reverse=True),
    label="y",
)
zero_state = []
if overflow_qubit is True:
    zero_state = VectorState(spec=encode(integer=0, num_systems=1), label="0")

augend_states = []
addend_states = []
carry_states = []
for i in range(0, encoding_depth):
    target_bit = i
    complement_bits = [n for n in range(0, encoding_depth) if n != target_bit]

    augend_state.partial_trace(complement_bits)
    addend_state.partial_trace(complement_bits)

    augend_bit = decode(augend_state.output())
    addend_bit = decode(addend_state.output())

    augend_bit_state = VectorState(
        spec=encode(integer=augend_bit, num_systems=1),
        label=augend_state.label + str(i),
    )
    addend_bit_state = VectorState(
        spec=encode(integer=addend_bit, num_systems=1),
        label=addend_state.label + str(i),
    )
    carry_state = VectorState(spec=encode(integer=0, num_systems=1), label="c" + str(i))

    augend_states.append(augend_bit_state)
    addend_states.append(addend_bit_state)
    carry_states.append(carry_state)

    augend_state.reset()
    addend_state.reset()

input_spec = flatten_list(
    [
        [carry_states[i], augend_states[i], addend_states[i]]
        for i in range(0, encoding_depth)
    ]
    + [zero_state]
)

# Gates

# Construct sequence of CARRY gates
carries = []
for i in range(0, encoding_depth - 1 + int(overflow_qubit)):
    system_shift = 3 * i

    ICCN = Not(
        targets=[system_shift + 3],
        controls=[system_shift + 1, system_shift + 2],
        num_systems=3 * encoding_depth + int(overflow_qubit),
    )
    ICNI = Not(
        targets=[system_shift + 2],
        controls=[system_shift + 1],
        num_systems=3 * encoding_depth + int(overflow_qubit),
    )
    CICN = Not(
        targets=[system_shift + 3],
        controls=[system_shift + 0, system_shift + 2],
        num_systems=3 * encoding_depth + int(overflow_qubit),
    )

    carry = [ICCN, ICNI, CICN]
    carries.append(carry)

CNOT = []
if overflow_qubit is True:
    system_shift = 3 * (encoding_depth - 1)
    CNOT = Not(
        targets=[system_shift + 2],
        controls=[system_shift + 1],
        num_systems=3 * encoding_depth + int(overflow_qubit),
    )

# Construct sequence of ANTICARRY and SUM gates
anticarries_sums = []
for i in range(0, encoding_depth):
    system_shift = 3 * (encoding_depth - 1 - i)

    if i != min(range(0, encoding_depth)):
        CICN = Not(
            targets=[system_shift + 3],
            controls=[system_shift + 0, system_shift + 2],
            num_systems=3 * encoding_depth + int(overflow_qubit),
        )
        ICNI = Not(
            targets=[system_shift + 2],
            controls=[system_shift + 1],
            num_systems=3 * encoding_depth + int(overflow_qubit),
        )
        ICCN = Not(
            targets=[system_shift + 3],
            controls=[system_shift + 1, system_shift + 2],
            num_systems=3 * encoding_depth + int(overflow_qubit),
        )

        anticarry = [CICN, ICNI, ICCN]
        anticarries_sums.append(anticarry)

    ICNI = Not(
        targets=[system_shift + 2],
        controls=[system_shift + 1],
        num_systems=3 * encoding_depth + int(overflow_qubit),
    )
    CINI = Not(
        targets=[system_shift + 2],
        controls=[system_shift + 0],
        num_systems=3 * encoding_depth + int(overflow_qubit),
    )

    summation = [ICNI, CINI]
    anticarries_sums.append(summation)

gates = flatten_list(carries + [CNOT] + anticarries_sums)

# Circuit
adder = QuantumCircuit(inputs=input_spec, gates=gates)
adder.diagram()

# Output
sum_registers = [3 * i + 2 for i in range(0, encoding_depth)]
sum_registers_complement = [
    i
    for i in range(0, 3 * encoding_depth + int(overflow_qubit))
    if i not in sum_registers
]
sum_state = adder.state(label="s", traces=sum_registers_complement)
sum_integer = decode(matrix=sum_state.output(), reverse=True)
sum_state = VectorState(spec=encode(integer=sum_integer, reverse=True), label="s")

# Results
augend_state.print()
addend_state.print()
sum_state.print()

final_time = time.time()
computation = f"Computation: {augend_integer} + {addend_integer} = {sum_integer}"
duration = f"Duration: {sp.N(final_time - initial_time,8).round(3)} seconds"
print(computation)
print(duration)

Output#

Diagram#

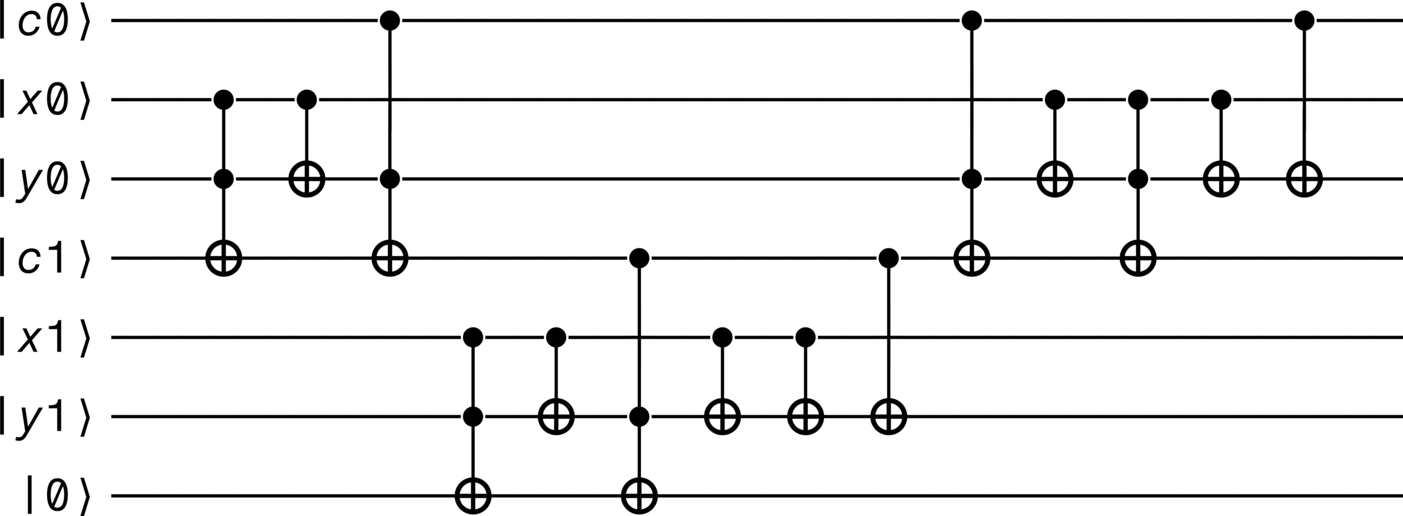
When overflow_qubit = True:

>>> adder.diagram()

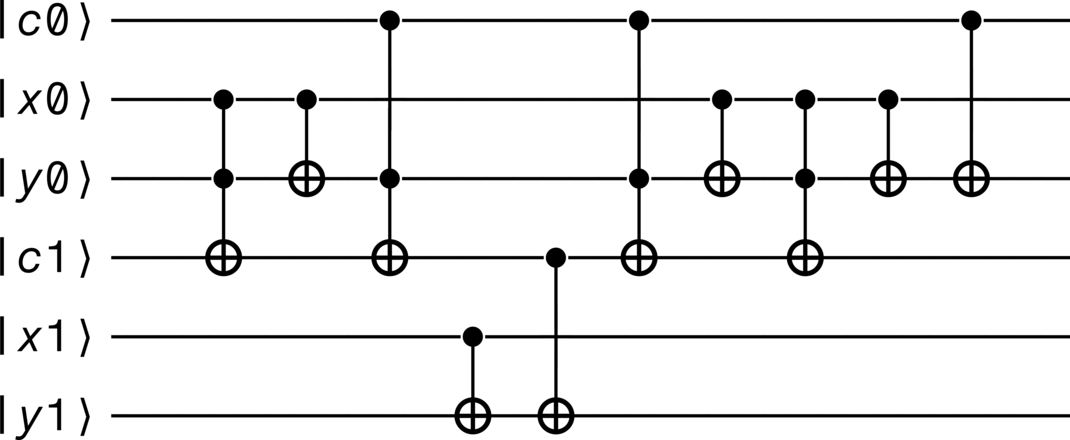
When overflow_qubit = False:

>>> adder.diagram()

States#

>>> augend_state.print()
|x⟩ = |1,0⟩

>>> addend_state.print()
|y⟩ = |1,0⟩

>>> sum_state.print()
|s⟩ = |0,1⟩

Results#

>>> print(computation)
Computation: 1 + 1 = 2

When overflow_qubit = True:

>>> print(duration)
Duration: 5.134 seconds

When overflow_qubit = False:

>>> print(duration)
Duration: 1.209 seconds

This version of a multi-qubit full adder is evidently much faster than the Ripple-carry adder for the equivalent number of qubits, which highlights the efficiency advantage of using fewer qubits to achieve the same computation.

References

[1]

V. Vedral, A. Barenco, and A. Ekert, “Quantum networks for elementary arithmetic operations”, Physical Review A, 54(1):147–153, July 1996. https://link.aps.org/doi/10.1103/PhysRevA.54.147, doi:10.1103/PhysRevA.54.147