Quantum state tomography via weak measurements

Description

The quantum state tomography methodology presented in Quantum state tomography is a standard scheme that uses ordinary (“strong”) measurements—those which by necessity disturb (i.e., collapse the wave function of) the quantum system under consideration. Thus, in order to perform state tomography without (significantly) disrupting the unknown system, we can use so-called weak measurements, that is, quantum measurements which minimize disturbance by leaving the measured state unaffected (to first order in the strength of the measurement). The idea of performing quantum state tomography using weak measurements constitutes a powerful technique that has been used with great success in a plethora of past experimental applications [19, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33].

The scheme presented here follows the work in [30]. It is limited to qubits, though is it thought to be generalizable to qudits without too much difficulty. Note that while most treatments consider weak measurements characterized by weakly coupled interactions (that is, unitary operators close to identity), this formalism is based on [34, 35], in which a near eigenstate of the NOT (Pauli-X) gate is perturbed weakly by a control state via the standard CNOT interaction. See, e.g., [23, 29, 36, 37, 38, 39] for pedagogical exposition of weak measurements and the associated weak values, and [20, 32, 36, 40] for good examples of weak-measurement tomography.

At the heart of this methodology is an ancillary qubit, which is also known as the target or probe. In the \(z\)-basis \(\left\{\ket{0},\ket{1}\right\}\), it may be expressed as

(352)\[\ket{\Probe} = \sqrt{\frac{1+\Strength}{2}}\ket{0} + \sqrt{\frac{1-\Strength}{2}}\ket{1}, \quad 0 \leq \Strength \leq 1.\]

Its function is to transform in response to the state of an unknown system \(\StateCV\). This is achieved by coupling the two states together, thereby enabling direct measurement of the ancilla to yield information regarding \(\StateCV\). If the interaction is sufficiently weak, then this state remains undisturbed. Note that of course, a quantum state cannot be fully characterized by performing just a single measurement. The best we can accomplish for qubits, at least using weak measurements, is to infer the expectation value of the unknown system along one of the three axes of the Bloch sphere. The original state \(\StateCV\) may then be completely reconstructed from the combined statistics, by way of the determination of the state’s Bloch vector.

Perhaps the simplest coupling between an unknown state and the probe that will permit this tomography scheme is the CNOT gate, which we write as

(353)\[\Control^0 \NOT^1 \equiv {\ket{0}\bra{0}}^0 \otimes \Identity^1 + {\ket{1}\bra{1}}^0 \otimes \Pauli_x^1.\]

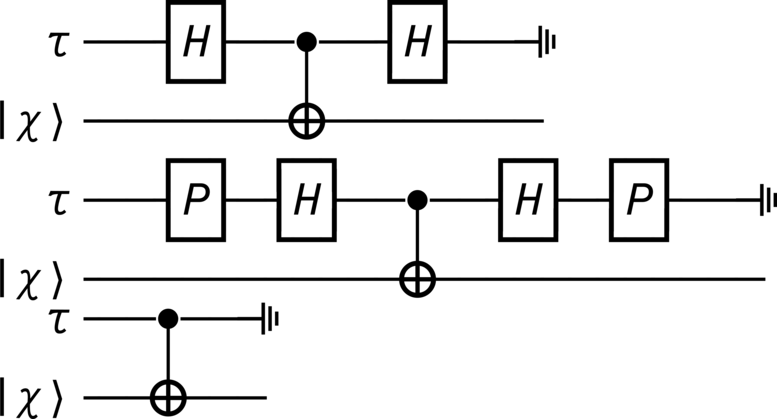
As we wish to measure along each of three Bloch axes, this can be combined with basis transformation gates \(\UnitaryBasis^{(\dagger)}_k\), yielding the system-probe unitary interaction

(354)\[\begin{split}\begin{aligned} \Tomography &= \bigl(\UnitaryBasis^{\dagger}_k \otimes \Identity\bigr) \cdot \Control^0 \NOT^1 \cdot \bigl(\UnitaryBasis_k \otimes \Identity\bigr) \\ &= \ket{0_k}\bra{0_k} \otimes \Identity + \ket{1_k}\bra{1_k} \otimes \Pauli_x. \end{aligned}\end{split}\]

This is depicted diagrammatically as a quantum circuit in Figure 26, where we denote the evolved ancilla by \(\StateProbe_k\). Here, the aforementioned basis gates \(\UnitaryBasis^{(\dagger)}_k\) (where \(k=1,2,3\)) represent transformations that map the \(z\)-basis eigenstates \(\left\{\ket{0},\ket{1}\right\}\) into either the \(x\)- (\(k=1\)), \(y\)- (\(k=2\)) or \(z\)- (\(k=3\)) bases. Specifically, we write

(355)\[\begin{split}\begin{aligned} \UnitaryBasis^\dagger_k \ket{0} &= \ket{0_k}, \\ \UnitaryBasis^\dagger_k \ket{1} &= \ket{1_k}, \end{aligned}\end{split}\]

where \(\left\{\ket{0_k},\ket{1_k}\right\}\) are eigenstates of the three bases of our qubit Hilbert space. This means that, given the Pauli matrices (130), the states defined by (355) necessarily satisfy

(356)\[\begin{split}\begin{aligned} \Pauli_k \ket{0_k} &= \ket{0_k}, \\ \Pauli_k \ket{1_k} &= -\ket{1_k}. \end{aligned}\end{split}\]

For this to be fulfilled, we must have

(357)\[\begin{split}\begin{aligned} \UnitaryBasis_1 &= \Hadamard, \\ \UnitaryBasis_2 &= \Hadamard \Phase^\dagger, \\ \UnitaryBasis_3 &= \Identity, \end{aligned}\end{split}\]

where

(358)\[\Hadamard \equiv \frac{1}{\sqrt{2}} \bigl(\ket{0}\bra{0} + \ket{0}\bra{1} + \ket{1}\bra{0} - \ket{1}\bra{1}\bigr)\]

is the Hadamard gate, and

(359)\[\Phase \equiv \ket{0}\bra{0} + \eye\ket{1}\bra{1}\]

is a phase shift gate.

Figure 26 A quantum state weak-measurement tomography algorithm.

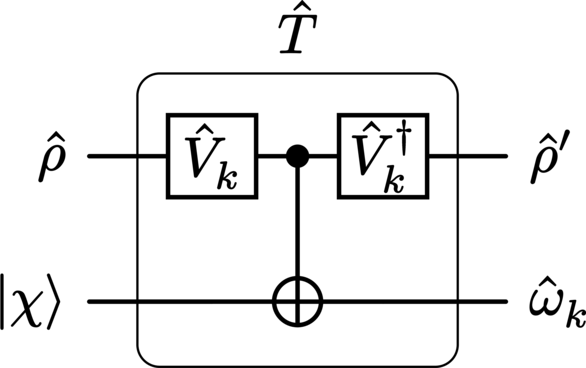
With these definitions in mind, a weak measurement can be easily computed in a number of steps. First, given the unknown system \(\StateCV\), the ancilla \(\ket{\Probe}\), and the weak-measurement unitary (354), the evolution of the product state \(\StateCV\otimes\ket{\Probe}\bra{\Probe}\) is the standard unitary map

(360)\[\begin{split}\begin{aligned} \MapGeneral_{\Tomography}\bigl[\StateCV\otimes\ket{\Probe}\bra{\Probe}\bigr] &= \Tomography\bigl(\StateCV\otimes\ket{\Probe}\bra{\Probe}\bigr)\Tomography^\dagger \\\ %= \; & \aket{0_k}\abra{0_k} \StateCV \aket{0_k}\abra{0_k} \otimes \aket{\Probe}\abra{\Probe} \\ %&+ \aket{0_k}\abra{0_k} \StateCV \aket{1_k}\abra{1_k} \otimes \aket{\Probe}\abra{\Probe}\Pauli_x \\ %&+ \aket{1_k}\abra{1_k} \StateCV \aket{0_k}\abra{0_k} \otimes \Pauli_x\aket{\Probe}\abra{\Probe} \\ %&+ \aket{1_k}\abra{1_k} \StateCV \aket{1_k}\abra{1_k} \otimes \Pauli_x\aket{\Probe}\abra{\Probe}\Pauli_x \\ &= \sum_{n,m=0}^{1} \ket{n_k}\bra{n_k} \StateCV \ket{m_k}\bra{m_k} \otimes \Pauli^n_x \ket{\Probe}\bra{\Probe} \Pauli_x^{m}. \end{aligned}\end{split}\]

The state of the evolved system \(\StateCV^\prime\) after the interaction is computed by performing a partial trace on the probe’s Hilbert space,

(361)\[\begin{split}\begin{aligned} \StateCV^\prime = \; & \trace_{1}\bigl[\Tomography\bigl(\StateCV\otimes\ket{\Probe}\bra{\Probe}\bigr)\Tomography^\dagger\bigr] \\ %= \; & \aket{0_k}\abra{0_k} \StateCV \aket{0_k}\abra{0_k} \\ %&+ \abra{\Probe}{\Pauli_x}\aket{\Probe} \aket{0_k}\abra{0_k} \StateCV \aket{1_k}\abra{1_k} \\ %&+ \abra{\Probe}{\Pauli_x}\aket{\Probe} \aket{1_k}\abra{1_k} \StateCV \aket{0_k}\abra{0_k} \\ %&+ \aket{1_k}\abra{1_k} \StateCV \aket{1_k}\abra{1_k}. = \; & \sum_{n,m=0}^{1} \bra{\Probe} \Pauli_x^{m} \Pauli_x^n \ket{\Probe} \cdot \ket{n_k}\bra{n_k} \StateCV \ket{m_k}\bra{m_k}. \end{aligned}\end{split}\]

To show that the measurement is necessarily weak, thereby leaving this evolved state unperturbed for sufficiently small \(\Strength\), we first use the definition of our normalized probe state (352) to compute

(362)\[\bra{\Probe} \Pauli_x \ket{\Probe} = \sqrt{1-\Strength^2}.\]

A Taylor series expansion of this lets us write

(363)\[\sqrt{1-\Strength^2} = 1 - \frac{\Strength^2}{2} + \mathcal{O}(\Strength^4),\]

with which we may express the evolved system (361) as

(364)\[\begin{split}\begin{aligned} \StateCV^\prime %=\; & \ket{0_k}\bra{0_k} \StateCV \ket{0_k}\bra{0_k} \\ %&+ \aket{0_k}\abra{0_k} \StateCV \aket{1_k}\abra{1_k} \\ %&+ \aket{1_k}\abra{1_k} \StateCV \aket{0_k}\abra{0_k} \\ %&+ \aket{1_k}\abra{1_k} \StateCV \aket{1_k}\abra{1_k} \\ %&- \left(\frac{\Strength^2}{2} - \mathcal{O}(\Strength^4)\right) \left[\aket{0_k}\abra{0_k} \StateCV \aket{1_k}\abra{1_k} + \aket{1_k}\abra{1_k} \StateCV \aket{0_k}\abra{0_k}\right] \\ %=\; & \sum_{n,m=0}^{1} \aket{n_k}\abra{n_k} \StateCV \aket{m_k}\abra{m_k} \\ %&- \left(\frac{\Strength^2}{2} - \mathcal{O}(\Strength^4)\right) \left[\aket{0_k}\abra{0_k} \StateCV \aket{1_k}\abra{1_k} + \aket{1_k}\abra{1_k} \StateCV \aket{0_k}\abra{0_k}\right] \\ =\; & \sum_{n,m=0}^{1} \ket{n_k}\bra{n_k} \StateCV \ket{m_k}\bra{m_k} + \mathcal{O}(\Strength^2). \end{aligned}\end{split}\]

By comparing this to our probe density, which can be expanded as

(365)\[\begin{split}\begin{aligned} \ket{\Probe}\bra{\Probe} %&= \Identity + \Strength\Pauli_z + \sqrt{1-\Strength^2}\Pauli_x, \\ %&= \ket{+}\bra{+} + \Strength\Pauli_z - \left(\frac{\Strength^2}{2} -\mathcal{O}(\Strength^4)\right)\Pauli_x, \\ &= \ket{+}\bra{+} + \frac{\Strength}{2}\Pauli_z + \mathcal{O}(\Strength^2), \end{aligned}\end{split}\]

it is easy to see that for sufficiently small \(\Strength\), e.g., \(\abs{\Strength} \ll 1\) such that \(\mathcal{O}(\Strength^2) \approx 0\), the system state (364) approximates its unperturbed form,

(366)\[\begin{split}\begin{aligned} \StateCV^\prime \approx\; & \sum_{n,m=0}^{1} \ket{n_k}\bra{n_k} \StateCV \ket{m_k}\bra{m_k} \\ %=\; & \aket{0_k}\abra{0_k} \StateCV \aket{0_k}\abra{0_k} \\ %&+ \aket{0_k}\abra{0_k} \StateCV \aket{1_k}\abra{1_k} \\ %&+ \aket{1_k}\abra{1_k} \StateCV \aket{0_k}\abra{0_k} \\ %&+ \aket{1_k}\abra{1_k} \StateCV \aket{1_k}\abra{1_k} \\ =\; & \StateCV, \end{aligned}\end{split}\]

while the probe (365), containing a first-order power of \(\Strength\), becomes

(367)\[\ket{\Probe}\bra{\Probe} \approx \ket{+}\bra{+} + \frac{\Strength}{2}\Pauli_z.\]

This is exactly what we desire, since if the probe were to become exactly an eigenstate of the Pauli-X operator \(\Pauli_x\), i.e.,

(368)\[\ket{\pm} \equiv \frac{1}{\sqrt{2}}\bigl(\ket{0} \pm \ket{1}\bigr),\]

then it would not be perturbed by the CNOT gate in its coupling (354) with the unknown system state. In other words, it would be unable to provide any information regarding \(\StateCV\), and would thus be tomographically useless. As however the probe state (365) does not assume the form of an eigenstate of \(\Pauli_x\) while the system remains unperturbed by the interaction (provided \(\Strength\) is sufficiently small), then we can in principle infer the state of \(\StateCV\) via strong measurements of the evolved ancilla state \(\StateProbe_k\) (for all \(k\)). This is the meaning of a weak measurement, and we call \(\Strength\) the strength of the measurement.

Let us now demonstrate how the qubit system \(\StateCV\) may be reconstructed by measuring the probe in the \(z\) basis. Starting with (360), we perform a partial trace on the first subsystem to obtain the evolved probe state,

(369)\[\begin{split}\begin{aligned} \StateProbe_k &\equiv \trace_{0}\bigl[\Tomography\bigl(\StateCV\otimes\ket{\Probe}\bra{\Probe}\bigr)\Tomography^\dagger\bigr] \\ %&= \abra{0_k} \StateCV \aket{0_k} \aket{\Probe}\abra{\Probe} + \abra{1_k} \StateCV \aket{1_k} \Pauli_x\aket{\Probe}\abra{\Probe}\Pauli_x \\ &= \sum_{n=0}^{1} \bra{n_k} \StateCV \ket{n_k} \cdot \Pauli^n_x \ket{\Probe}\bra{\Probe} \Pauli_x^{n}. \end{aligned}\end{split}\]

Computing the expectation value of \(\Pauli_z\) for this form then yields

(370)\[\begin{split}\begin{aligned} \trace[\Pauli_z\StateProbe_k] &= \bra{0} \StateProbe_k \ket{0} - \bra{1} \StateProbe_k \ket{1} \\ &= \Strength \bigl(\bra{0_k} \StateCV \ket{0_k} - \bra{1_k} \StateCV \ket{1_k}\bigr) \\ &= \Strength \, \trace[\Pauli_k \StateCV], \end{aligned}\end{split}\]

where we used the fact that

(371)\[\Pauli_k = \ket{0_k}\bra{0_k} - \ket{1_k}\bra{1_k}.\]

Rescaling by a factor \(\tfrac{1}{\Strength}\) then allows us to make the connection between performing a \(z\)-basis measurement on the probe state (369) and inferring the expectation value of \(\Pauli_k\) for the state of the unknown system. This is because, up to the factor \(\Strength\), the two operations are equivalent. Note that, for brevity, we will write

(372)\[\Expectation_k \equiv \frac{1}{\Strength}\trace[\Pauli_z\StateProbe_k] = \trace[\Pauli_k \StateCV],\]

which is often denoted in the literature as \(\big<\Pauli_k\big>\).

If we define \(\Pauli_0 \equiv \Identity\), then the set of operators \(\{\Pauli_k\}_{k=0}^3\) forms a complete basis for the space of complex \(2 \times 2\) matrices. Since this coincides with the space of linear operators \(\SpaceLinear(\SpaceHilbert)\) on our qubit (\(2\)-dimensional) Hilbert space \(\SpaceHilbert\), then any state \(\StateCV \in \SpaceLinear(\SpaceHilbert)\) can accordingly be reconstructed via the linear combination,

(373)\[ \StateCV = \frac{1}{2}\sum_{k=0}^{3} \trace[\Pauli_k \StateCV] \Pauli_k.\]

Since the coefficient for \(k = 0\) is fixed by normalization (i.e., \(\trace[\Pauli_0 \StateCV] = 1\)), then the state is completely (and uniquely) determined by the Bloch vector, which is defined for a \(\Dimension\)-dimensional state as the \((\Dimension^2-1)\)-dimensional real vector of parameters \(\bigl\{\trace[\Pauli_k \StateCV]\bigr\}_{k = 1}^{\Dimension^2 - 1}\). Accordingly, the linear combination (373) is said to be the Bloch sphere representation of the state \(\StateCV\). Thus, since we have shown that we can infer expectation values (372) for an unknown state by coupling it with a probe via a CNOT and subsequently performing a measurement of the probe in the \(z\)-basis, then we can characterize the state completely without directly measuring it.

Implementation

Listing 26 /text/examples/algorithms/tomography_weak.py

from qhronology.quantum.states import VectorState, MatrixState
from qhronology.quantum.gates import Not, Hadamard, Phase, Pauli
from qhronology.quantum.circuits import QuantumCircuit
from qhronology.utilities.helpers import flatten_list

import sympy as sp

# Input
tau = sp.MatrixSymbol("τ", 2, 2).as_mutable()
unknown_state = MatrixState(spec=tau, label="τ")

probe_state = VectorState(
    spec=[("sqrt((1 + ε)/2)", [0]), ("sqrt((1 - ε)/2)", [1])],
    symbols={"ε": {"real": True, "nonnegative": True}},
    conditions=[
        ("ε", "1 - ε"),
        ("ε", "1 - ε"),
    ],  # Describes the fact that ε is between 0 and 1 (inclusive)
    label="χ",
)

# Gates
CN = Not(targets=[1], controls=[0], num_systems=2)
HI = Hadamard(targets=[0], num_systems=2)
PI = Phase(exponent=1 / 2, targets=[0], num_systems=2)

VI = [[HI], [PI, HI], []]

# Circuits
evolved_probe_states = []
for gates in VI:
    gates_pre = gates
    gates_post = gates[::-1]
    for gate in gates_post:
        gate.conjugate = True

    tomography = QuantumCircuit(
        inputs=[unknown_state, probe_state],
        gates=flatten_list([gates_pre, CN, gates_post]),
        traces=[0],
    )
    tomography.diagram()
    evolved_probe_state = tomography.state(label="ω")
    evolved_probe_states.append(evolved_probe_state)

# Weak-measurement quantum state tomography
Z = Pauli(index=3, targets=[0], num_systems=1)
expectations = []
expectations.append(1)  # Expectation value corresponding to the identity operator
for state in evolved_probe_states:
    state.coefficient("1/ε")
    statistics = state.measure(
        operators=[Z], targets=[0], statistics=True, observable=True
    )
    expectation = statistics[0]
    expectations.append(expectation)

# Reconstruct state via Bloch-sphere representation using weak measurements
pauli_matrices = [
    Pauli(index=i, targets=[0], num_systems=1).output() for i in range(0, 4)
]
spec = sp.zeros(2)
for i in range(0, 4):
    spec += expectations[i] * pauli_matrices[i]
reconstructed_state = MatrixState(
    spec=sp.Matrix(spec),
    conditions=[(tau[1, 1], 1 - tau[0, 0]), (1 - tau[0, 0], tau[1, 1])],
    label="τ",
)
reconstructed_state.coefficient(sp.Rational(1, 2))  # Manually normalize
reconstructed_state.simplify()

# Results
unknown_state.print()
reconstructed_state.print()

Output

Diagram

>>> tomography.diagram()

States

>>> unknown_state.print()
τ = τ[0, 0]|0⟩⟨0| + τ[0, 1]|0⟩⟨1| + τ[1, 0]|1⟩⟨0| + τ[1, 1]|1⟩⟨1|

>>> reconstructed_state.print()
τ = τ[0, 0]|0⟩⟨0| + τ[0, 1]|0⟩⟨1| + τ[1, 0]|1⟩⟨0| + τ[1, 1]|1⟩⟨1|

References

[1]

J. M. Knight and L. Vaidman, “Weak measurement of photon polarization”, Physics Letters A, 143(8):357–361, January 1990. https://www.sciencedirect.com/science/article/pii/037596019090371T, doi:10.1016/0375-9601(90)90371-T

[2]

J.g. Story, N.w.m. Ritchie, and R.g. Hulet, “Weak measurements”, Modern Physics Letters B, 05(26):1713–1725, November 1991. https://www.worldscientific.com/doi/abs/10.1142/S0217984991002069, doi:10.1142/S0217984991002069

[3]

S. Wu and K. Mølmer, “Weak measurements with a qubit meter”, Physics Letters A, 374(1):34–39, December 2009. https://www.sciencedirect.com/science/article/pii/S0375960109012882, doi:10.1016/j.physleta.2009.10.026

[4]

A. G. Kofman, S. Ashhab, and F. Nori, “Nonperturbative theory of weak pre- and post-selected measurements”, Physics Reports, 520(2):43–133, November 2012. https://www.sciencedirect.com/science/article/pii/S0370157312002050, doi:10.1016/j.physrep.2012.07.001

[5]

L. G. Bishop, F. Costa, and T. C. Ralph, “Quantum state tomography on closed timelike curves using weak measurements”, Classical and Quantum Gravity, 42(4):045018, February 2025. https://dx.doi.org/10.1088/1361-6382/ada90b, doi:10.1088/1361-6382/ada90b

[6]

O. Hosten and P. Kwiat, “Observation of the Spin Hall Effect of Light via Weak Measurements”, Science, 319(5864):787–790, February 2008. https://www.science.org/doi/10.1126/science.1152697, doi:10.1126/science.1152697

[7]

J. S. Lundeen and A. M. Steinberg, “Experimental Joint Weak Measurement on a Photon Pair as a Probe of Hardy's Paradox”, Physical Review Letters, 102(2):020404, January 2009. https://link.aps.org/doi/10.1103/PhysRevLett.102.020404, doi:10.1103/PhysRevLett.102.020404

[8]

P. B. Dixon, D. J. Starling, A. N. Jordan, and J. C. Howell, “Ultrasensitive Beam Deflection Measurement via Interferometric Weak Value Amplification”, Physical Review Letters, 102(17):173601, April 2009. https://link.aps.org/doi/10.1103/PhysRevLett.102.173601, doi:10.1103/PhysRevLett.102.173601

[9]

Y.-S. Kim, Y.-W. Cho, Y.-S. Ra, and Y.-H. Kim, “Reversing the weak quantum measurement for a photonic qubit”, Optics Express, 17(14):11978–11985, July 2009. https://opg.optica.org/oe/abstract.cfm?uri=oe-17-14-11978, doi:10.1364/OE.17.011978

[10]

Y.-W. Cho, H.-T. Lim, Y.-S. Ra, and Y.-H. Kim, “Weak value measurement with an incoherent measuring device”, New Journal of Physics, 12(2):023036, February 2010. https://dx.doi.org/10.1088/1367-2630/12/2/023036, doi:10.1088/1367-2630/12/2/023036

[11]

M. E. Goggin, M. P. Almeida, M. Barbieri, B. P. Lanyon, J. L. O’Brien, A. G. White, and G. J. Pryde, “Violation of the Leggett–Garg inequality with weak measurements of photons”, Proceedings of the National Academy of Sciences, 108(4):1256–1261, January 2011. https://www.pnas.org/doi/full/10.1073/pnas.1005774108, doi:10.1073/pnas.1005774108

[12]

O. Zilberberg, A. Romito, and Y. Gefen, “Charge Sensing Amplification via Weak Values Measurement”, Physical Review Letters, 106(8):080405, February 2011. https://link.aps.org/doi/10.1103/PhysRevLett.106.080405, doi:10.1103/PhysRevLett.106.080405

[13]

J. S. Lundeen, B. Sutherland, A. Patel, C. Stewart, and C. Bamber, “Direct measurement of the quantum wavefunction”, Nature, 474(7350):188–191, June 2011. http://www.nature.com/articles/nature10120, doi:10.1038/nature10120

[14]

S. Kocsis, B. Braverman, S. Ravets, M. J. Stevens, R. P. Mirin, L. K. Shalm, and A. M. Steinberg, “Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer”, Science, 332(6034):1170–1173, June 2011. https://www.science.org/doi/10.1126/science.1202218, doi:10.1126/science.1202218

[15]

A. Feizpour, X. Xing, and A. M. Steinberg, “Amplifying Single-Photon Nonlinearity Using Weak Measurements”, Physical Review Letters, 107(13):133603, September 2011. https://link.aps.org/doi/10.1103/PhysRevLett.107.133603, doi:10.1103/PhysRevLett.107.133603

[16]

Y.-S. Kim, J.-C. Lee, O. Kwon, and Y.-H. Kim, “Protecting entanglement from decoherence using weak measurement and quantum measurement reversal”, Nature Physics, 8(2):117–120, February 2012. http://www.nature.com/articles/nphys2178, doi:10.1038/nphys2178

[17]

L. A. Rozema, A. Darabi, D. H. Mahler, A. Hayat, Y. Soudagar, and A. M. Steinberg, “Violation of Heisenberg's Measurement-Disturbance Relationship by Weak Measurements”, Physical Review Letters, 109(10):100404, September 2012. https://link.aps.org/doi/10.1103/PhysRevLett.109.100404, doi:10.1103/PhysRevLett.109.100404

[18]

R. Vijay, C. Macklin, D. H. Slichter, S. J. Weber, K. W. Murch, R. Naik, A. N. Korotkov, and I. Siddiqi, “Stabilizing Rabi oscillations in a superconducting qubit using quantum feedback”, Nature, 490(7418):77–80, October 2012. http://www.nature.com/articles/nature11505, doi:10.1038/nature11505

[19]

M. Hatridge, S. Shankar, M. Mirrahimi, F. Schackert, K. Geerlings, T. Brecht, K. M. Sliwa, B. Abdo, L. Frunzio, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, “Quantum Back-Action of an Individual Variable-Strength Measurement”, Science, 339(6116):178–181, January 2013. https://www.science.org/doi/10.1126/science.1226897, doi:10.1126/science.1226897

[20]

J. Z. Salvail, M. Agnew, A. S. Johnson, E. Bolduc, J. Leach, and R. W. Boyd, “Full characterization of polarization states of light via direct measurement”, Nature Photonics, 7(4):316–321, April 2013. http://www.nature.com/articles/nphoton.2013.24, doi:10.1038/nphoton.2013.24

[21]

J. P. Groen, D. Ristè, L. Tornberg, J. Cramer, P. C. de Groot, T. Picot, G. Johansson, and L. DiCarlo, “Partial-Measurement Backaction and Nonclassical Weak Values in a Superconducting Circuit”, Physical Review Letters, 111(9):090506, August 2013. https://link.aps.org/doi/10.1103/PhysRevLett.111.090506, doi:10.1103/PhysRevLett.111.090506

[22]

M. Malik, M. Mirhosseini, M. P. J. Lavery, J. Leach, M. J. Padgett, and R. W. Boyd, “Direct measurement of a 27-dimensional orbital-angular-momentum state vector”, Nature Communications, 5(1):3115, January 2014. http://www.nature.com/articles/ncomms4115, doi:10.1038/ncomms4115

[23]

M. S. Blok, C. Bonato, M. L. Markham, D. J. Twitchen, V. V. Dobrovitski, and R. Hanson, “Manipulating a qubit through the backaction of sequential partial measurements and real-time feedback”, Nature Physics, 10(3):189–193, March 2014. http://www.nature.com/articles/nphys2881, doi:10.1038/nphys2881

[24]

O. S. Magaña-Loaiza, M. Mirhosseini, B. Rodenburg, and R. W. Boyd, “Amplification of Angular Rotations Using Weak Measurements”, Physical Review Letters, 112(20):200401, May 2014. https://link.aps.org/doi/10.1103/PhysRevLett.112.200401, doi:10.1103/PhysRevLett.112.200401

[25]

T. Denkmayr, H. Geppert, S. Sponar, H. Lemmel, A. Matzkin, J. Tollaksen, and Y. Hasegawa, “Observation of a quantum Cheshire Cat in a matter-wave interferometer experiment”, Nature Communications, 5(1):4492, July 2014. http://www.nature.com/articles/ncomms5492, doi:10.1038/ncomms5492

[26]

M. Mirhosseini, O. S. Magaña-Loaiza, S. M. Hashemi Rafsanjani, and R. W. Boyd, “Compressive Direct Measurement of the Quantum Wave Function”, Physical Review Letters, 113(9):090402, August 2014. https://link.aps.org/doi/10.1103/PhysRevLett.113.090402, doi:10.1103/PhysRevLett.113.090402

[27]

Z. Shi, M. Mirhosseini, J. Margiewicz, M. Malik, F. Rivera, Z. Zhu, and R. W. Boyd, “Scan-free direct measurement of an extremely high-dimensional photonic state”, Optica, 2(4):388–392, April 2015. https://opg.optica.org/optica/abstract.cfm?uri=optica-2-4-388, doi:10.1364/OPTICA.2.000388

[28]

D. H. Mahler, L. Rozema, K. Fisher, L. Vermeyden, K. J. Resch, H. M. Wiseman, and A. Steinberg, “Experimental nonlocal and surreal Bohmian trajectories”, Science Advances, February 2016. https://www.science.org/10.1126/sciadv.1501466, doi:10.1126/sciadv.1501466

[29]

G. S. Thekkadath, L. Giner, Y. Chalich, M. J. Horton, J. Banker, and J. S. Lundeen, “Direct Measurement of the Density Matrix of a Quantum System”, Physical Review Letters, 117(12):120401, September 2016. https://link.aps.org/doi/10.1103/PhysRevLett.117.120401, doi:10.1103/PhysRevLett.117.120401

[30]

F. Piacentini, A. Avella, M. P. Levi, M. Gramegna, G. Brida, I. P. Degiovanni, E. Cohen, R. Lussana, F. Villa, A. Tosi, F. Zappa, and M. Genovese, “Measuring Incompatible Observables by Exploiting Sequential Weak Values”, Physical Review Letters, 117(17):170402, October 2016. https://link.aps.org/doi/10.1103/PhysRevLett.117.170402, doi:10.1103/PhysRevLett.117.170402

[31]

M. Hallaji, A. Feizpour, G. Dmochowski, J. Sinclair, and A. M. Steinberg, “Weak-value amplification of the nonlinear effect of a single photon”, Nature Physics, 13(6):540–544, June 2017. http://www.nature.com/articles/nphys4040, doi:10.1038/nphys4040

[32] (1,2)

Y. Kim, Y.-S. Kim, S.-Y. Lee, S.-W. Han, S. Moon, Y.-H. Kim, and Y.-W. Cho, “Direct quantum process tomography via measuring sequential weak values of incompatible observables”, Nature Communications, 9(1):192, January 2018. https://www.nature.com/articles/s41467-017-02511-2, doi:10.1038/s41467-017-02511-2

[33]

G. Nirala, S. N. Sahoo, A. K. Pati, and U. Sinha, “Measuring average of non-Hermitian operator with weak value in a Mach-Zehnder interferometer”, Physical Review A, 99(2):022111, February 2019. https://link.aps.org/doi/10.1103/PhysRevA.99.022111, doi:10.1103/PhysRevA.99.022111

[34]

G. J. Pryde, J. L. O’Brien, A. G. White, S. D. Bartlett, and T. C. Ralph, “Measuring a Photonic Qubit without Destroying It”, Physical Review Letters, 92(19):190402, May 2004. https://link.aps.org/doi/10.1103/PhysRevLett.92.190402, doi:10.1103/PhysRevLett.92.190402

[35]

G. J. Pryde, J. L. O’Brien, A. G. White, T. C. Ralph, and H. M. Wiseman, “Measurement of Quantum Weak Values of Photon Polarization”, Physical Review Letters, 94(22):220405, June 2005. https://link.aps.org/doi/10.1103/PhysRevLett.94.220405, doi:10.1103/PhysRevLett.94.220405

[36] (1,2)

S. Wu, “State tomography via weak measurements”, Scientific Reports, 3(1):1193, February 2013. https://www.nature.com/articles/srep01193, doi:10.1038/srep01193

[37]

B. E. Y. Svensson, “Pedagogical Review of Quantum Measurement Theory with an Emphasis on Weak Measurements”, Quanta, 2(1):18–49, May 2013. http://quanta.ws/ojs/index.php/quanta/article/view/12, doi:10.12743/quanta.v2i1.12

[38]

B. Tamir and E. Cohen, “Introduction to Weak Measurements and Weak Values”, Quanta, 2(1):7–17, May 2013. http://quanta.ws/ojs/index.php/quanta/article/view/14, doi:10.12743/quanta.v2i1.14

[39]

J. Dressel, M. Malik, F. M. Miatto, A. N. Jordan, and R. W. Boyd, “Colloquium: Understanding quantum weak values: Basics and applications”, Reviews of Modern Physics, 86(1):307–316, March 2014. https://link.aps.org/doi/10.1103/RevModPhys.86.307, doi:10.1103/RevModPhys.86.307

[40]

A. Botero, “Weak value tomography of strong quantum measurements”, Quantum Studies: Mathematics and Foundations, 5(3):423–437, September 2018. https://doi.org/10.1007/s40509-018-0155-0, doi:10.1007/s40509-018-0155-0