Equivalent-circuit picture for D-CTCs

Description

This algorithm implements the equivalent-circuit picture (ECP, see Iterative picture: The equivalent circuit) of D-CTCs. In its current form, it is not a particularly useful example, having very general input state and unitary matrix symbolic representations that make any subsequent analysis infeasible. Instead, the algorithm is included simply because it is an interesting demonstration of advanced usage of Qhronology. Note that the larger the number of algebraic symbols (and associated conditions) that are contained within the states and gates, the higher the complexity of the internal calculations, resulting in correspondingly longer computation times.

Figure 33 The equivalent-circuit picture of a D-CTC.

Implementation

The desired number of iterations can be changed by setting iterations to an appropriate positive integer.

Listing 31 /text/examples/ctcs/ecp.py

from qhronology.quantum.states import MixedState
from qhronology.quantum.gates import QuantumGate
from qhronology.quantum.circuits import QuantumCircuit

import sympy as sp
from sympy.physics.quantum.dagger import Dagger

iterations = 1
dimensionality = 2

# Input
rho = sp.MatrixSymbol("ρ", dimensionality, dimensionality).as_mutable()
respecting_state = MixedState(
    spec=rho, dim=dimensionality, conditions=[(sp.trace(rho), 1)], label="ρ"
)
seed_state = MixedState(
    spec=sp.eye(dimensionality), dim=dimensionality, norm=1, label="τ_0"
)

# Gate
unitary = sp.MatrixSymbol("U", dimensionality**2, dimensionality**2).as_mutable()
U = QuantumGate(spec=unitary, targets=[0, 1], num_systems=2, dim=dimensionality)

# Construct conditions
conditions_respecting = [(sp.trace(rho), 1)]
conditions_unitary = [
    ((unitary * Dagger(unitary))[n], (sp.eye(dimensionality**2))[n])
    for n in range(0, len(unitary))
]
conditions = conditions_respecting + conditions_unitary

# Circuit
violating_state = seed_state
for n in range(1, iterations + 1):
    iteration = QuantumCircuit(
        inputs=[respecting_state, violating_state],
        gates=[U],
        conditions=conditions,
        traces=[0],
    )
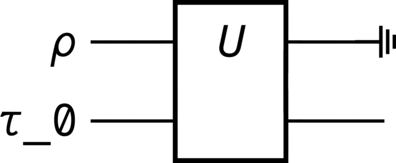
    iteration.diagram(pad=(1, 0), sep=(0, 1), style="unicode")
    violating_state = iteration.state(label=f"τ_{n}")

# Output
final_state = violating_state

# Results
seed_state.print()

Output

Diagram

>>> iteration.diagram()

States

>>> seed_state.print()
τ_0 = 1/2|0⟩⟨0| + 1/2|1⟩⟨1|